당니의 개발자 스토리
2주차 개념 #9. 깊이우선탐색(DFS, Depth First Search) 본문
2주차 개념 #9. 깊이우선탐색(DFS, Depth First Search)
clainy 2024. 3. 24. 21:212주차 개념 #9. 깊이우선탐색(DFS, Depth First Search)
오늘은 깊이 우선 탐색(DFS, Depth First Search)에 대해서 얘기를 해보도록 할게요.

DFS는 그래프를 탐색할 때 쓰는 알고리즘이고요. 어떤 노드부터 시작해서 인접한 노드들을 재귀적으로 방문하며, 방문한 정점은 다시 방문하지 않으며 각 분기마다 가능한 가장 멀리 있는 노드까지 탐색하는 알고리즘 입니다.
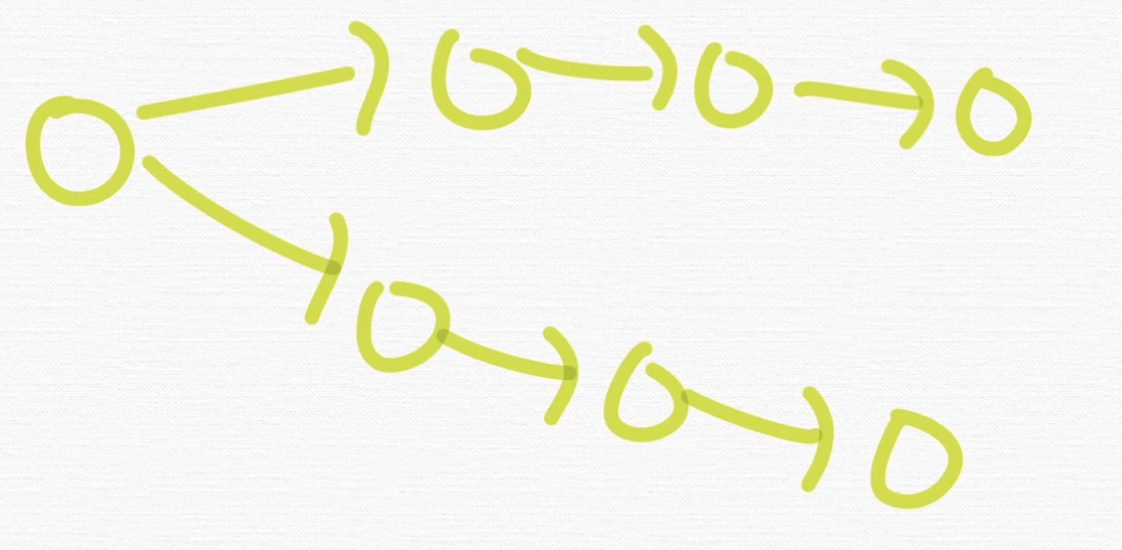
만약에 이런 그래프가 있다고 할게요.
우리가 BFS를 배우지 않았지만, BFS라면

이런 식으로 탐색을 하거든요. level별로 탐색을 해요. 이런 식으로 방문하면서 정점들을 탐색해 나가는 게 BFS인데, DFS는 이렇게 탐색을 하지 않고요. 어떻게 탐색하냐?

바로 이런 식으로 탐색해요. 이렇게 이 노드를 방문하고 더 깊게 들어가! 더 깊게 들어가! 해서 이 분기에서 가장 멀리 있는 노드까지 탐색을 하고,
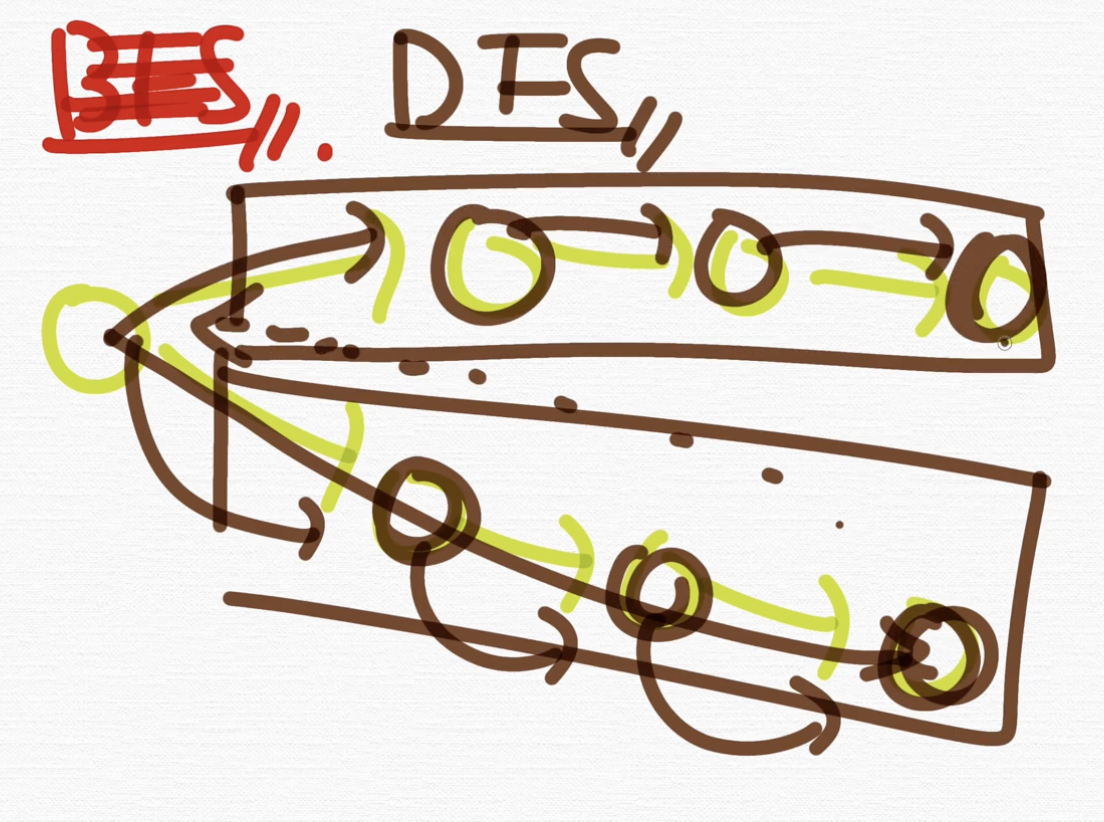
다시 돌아와서 그 다음 분기에 가서 똑같이 재귀적으로 방문해서 깊이 있는 노드까지 탐색을 하는 그런 알고리즘 입니다.
분기라는 말이 좀 생소할 수 있는데,

분기는 그냥 두 개 이상으로 정점이 쪼개진다. 이걸 이제 하나의 분기라고 놓을 수 있어요.
이런 식으로 각 분기마다 가장 멀리 있는 노드까지 탐색을 하고요. 지금 보시는 것처럼 방문한 정점을 다시 방문하지 않죠. DFS는 방문한 정점은 다시 방문하지 않아요. 이런 특징도 가지고 있는 알고리즘이 DFS, Depth First Search, 가장 깊게 탐색하는 알고리즘이라고 보시면 됩니다.
차근차근 얘기를 해볼 테니까 따라오시면 돼요.
먼저 수도코드를 볼게요.

사실 어떤 알고리즘을 이해한다라고 했을 때 수도코드를 이해하면, 그 알고리즘을 이해한 거에요. DFS의 수도코드를 볼게요.
참고로 수도코드는 프로그램의 로직을 표현하기 위해 쓰는 코드구요.
주로 어떤 알고리즘이 어떠한 로직을 갖고 있는지 나타내기 위해서 쓰는 코드를 수도코드 라고 합니다.

하나씩 살펴보면,
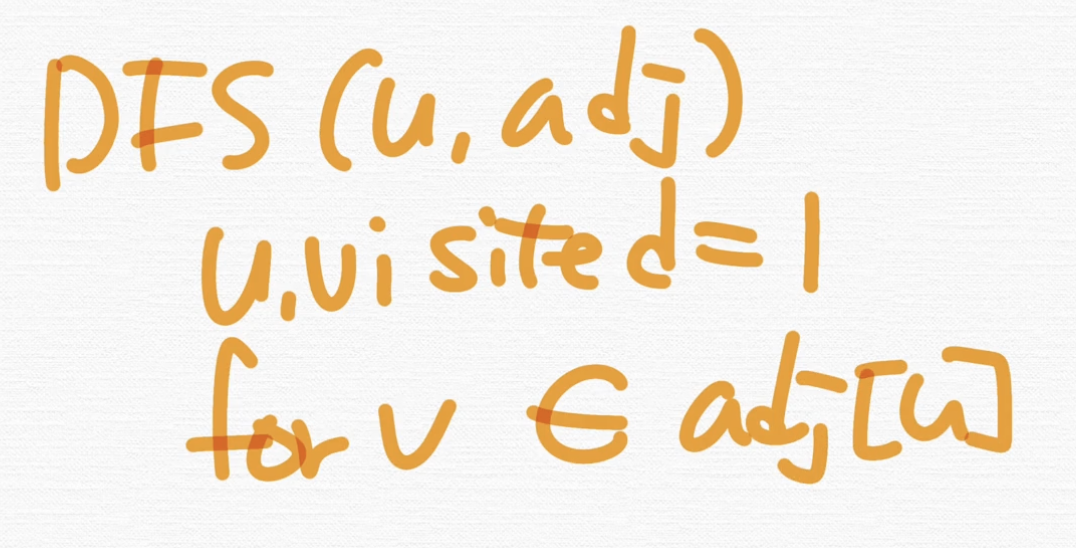
u로부터 v인데, u를 방문했다고 색칠한 다음에 그 노드와 인접해 있는 v를 살펴보는 거죠. adj는 인접리스트고, u는 from, v는 to라고 했습니다.

이런 식의 그래프가 있다고 했을 때, 이 노드들을 하나하나 방문하면서 방문 안 한 노드만 탐색한다고 했죠.
만약에 이 노드가 방문이 안 되어있다 그러면

이렇게 호출을 하는 알고리즘 입니다. 지금 보시면 재귀적인 알고리즘이고 이 정도 코드는 외워주셔야 돼요. 4줄만 외우시고 이해를 하시면 정말 여러분들이 DFS를 바르게 공부하신 것과 다름이 없습니다.
∈ 기호는 포함되어 있다 라는 수학적 기호예요. 그러니까 인접 리스트에 있는 정점들을 다 탐색한다라는 의미예요. u로부터 인접해있는 노드들을 탐색을 하면서 방문하는 정점을 이런 식으로 재귀적으로 호출하는 단순한 수도코드죠.
이 수도코드를 봐도 이해가 안 됐다? 걱정하지 마십시오. 제가 준비를 많이 했습니다.

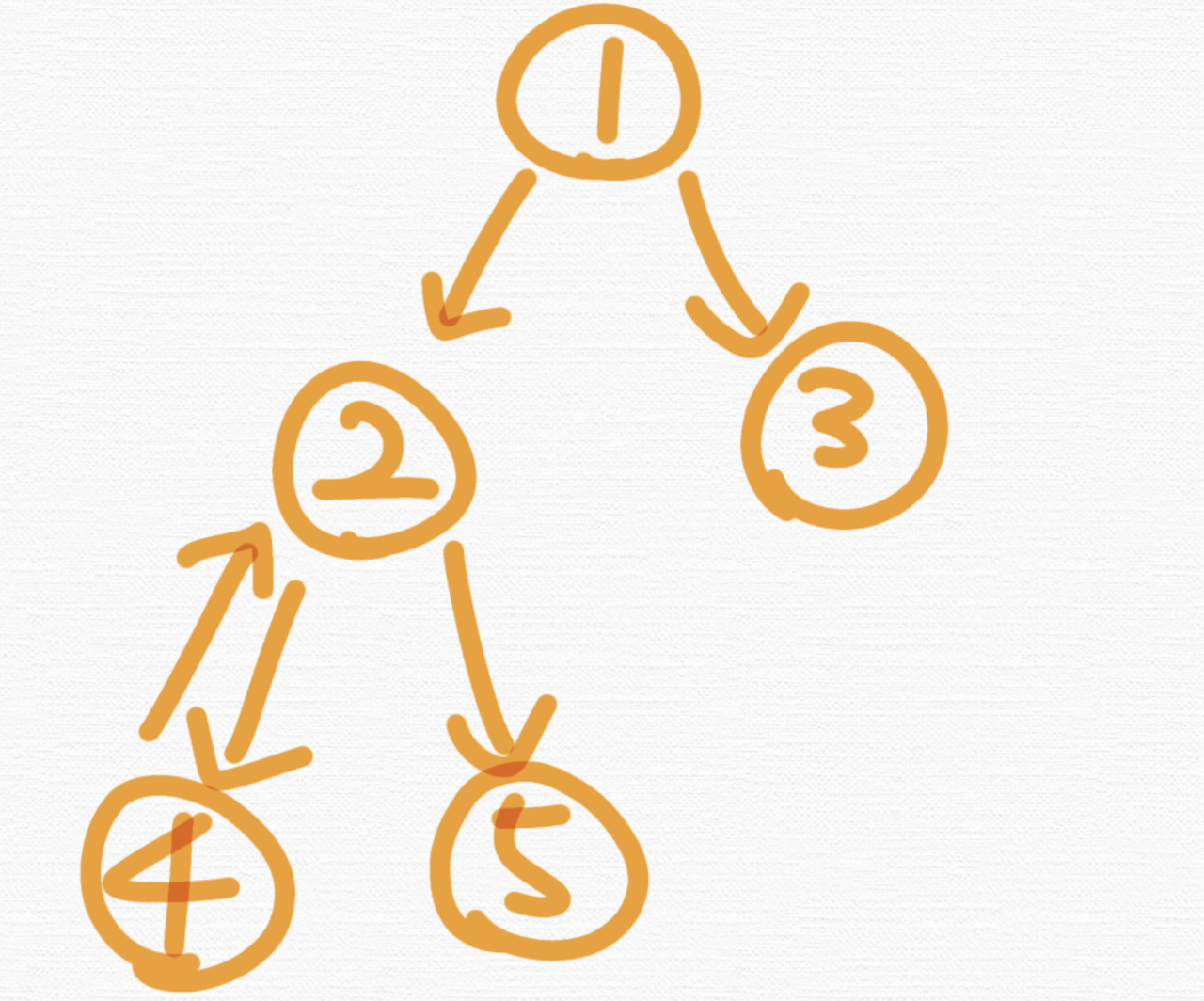
이런 그래프가 있다고 할게요.
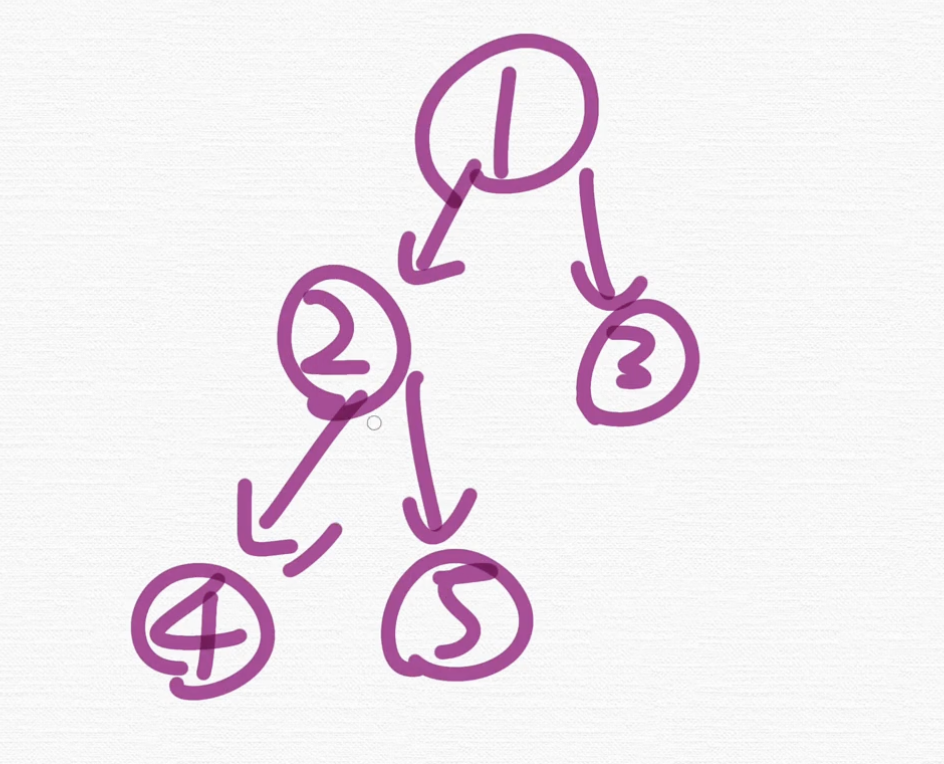
이 그래프에서 DFS로 탐색을 할 겁니다.

이걸 이제 DFS로 방문한다고 해볼게요. 그럼 어떻게 되냐?
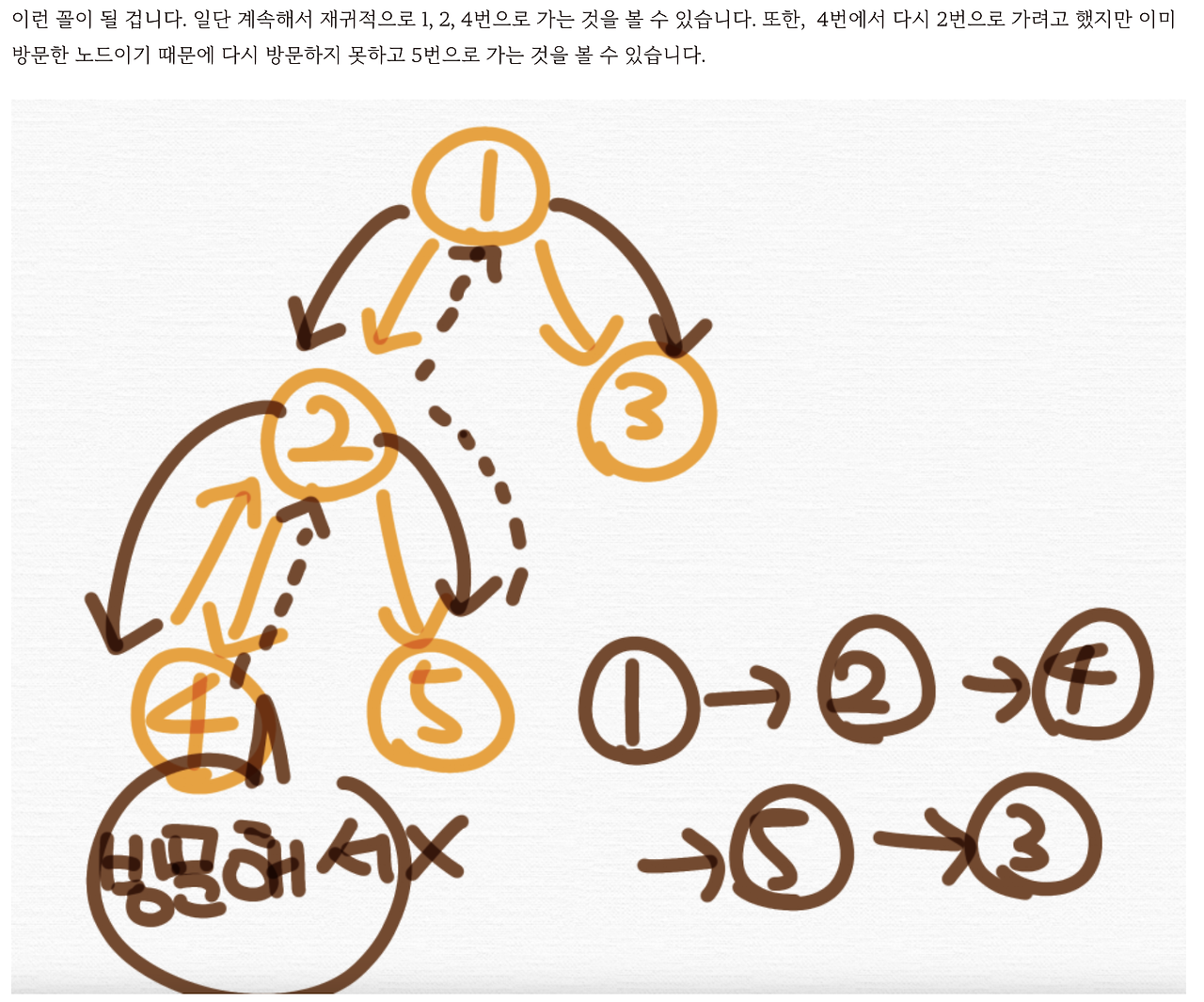
1 -> 2 -> 4 이렇게 깊게 탐색하고 4에서 2로 가려고 하니까 방문한 노드는 방문하지 않으니까 반환하고, 2에서 다시 분기, 5까지 처리를 합니다. 그리고 그 다음에는 1번에서 3까지 이렇게 방문하겠죠. 이 그래프를 DFS로 탐색하는 경우 이렇게 됩니다.
자 이거를 코드를 통해서 이해를 해보도록 할게요.

자 오늘은 디버깅까지 해볼거에요. 자 이런 코드에요.

이거는 이해하시죠?

이걸 인접리스트로 나타낸 겁니다. 우리가 dfs(1) 부터 시작한다고 해볼게요.

DFS가 무조건 이 루트노드부터 시작할 필요는 없어요. 임의의 노드부터 시작을 해도 되는데 일단 예제는 루트노드부터 시작하는 DFS를 했다라는 것을 참고해 주시면 되고요.
이 DFS 코드와 수도코드를 비교해볼게요.
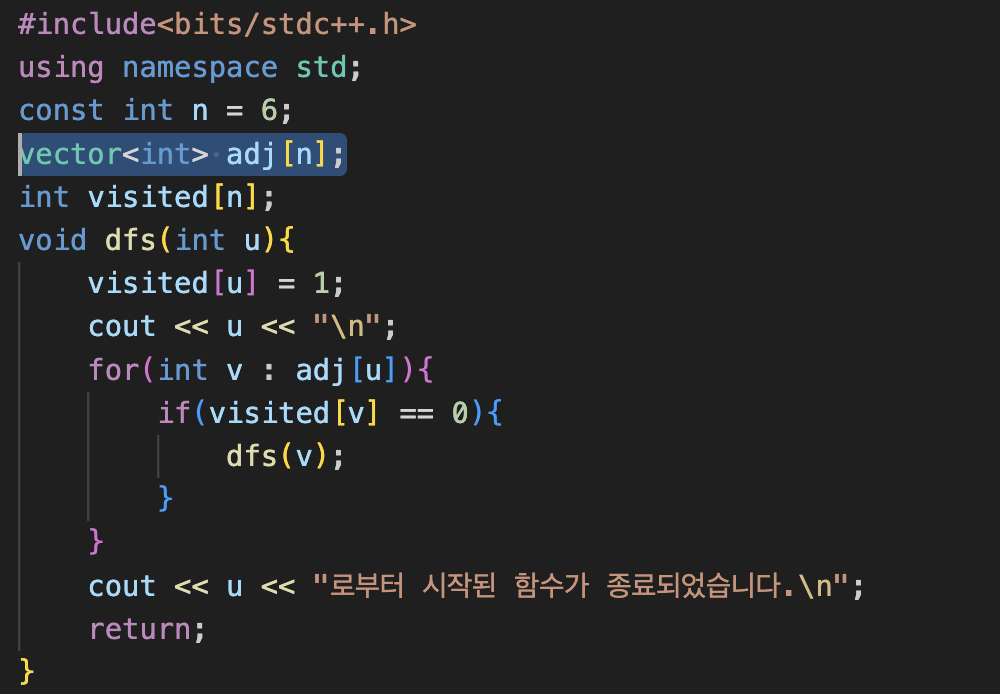
일단은 Adjacent vector는 전역변수로 놨기 때문에 지역변수, 매개변수로 받을 필요가 없죠.

그래서 수도코드랑 달리, adj를 따로 받을 필요가 없습니다. 그리고 어떤 정점을 방문했는지 안 했는지를 표현하는 배열. visited 배열을 쓰면 되는 거예요.

그리고 나서 이 u로부터 인접해 있는 간선들, 이 수도코드를 보고 코드를 구축할 수 있어야 돼요.
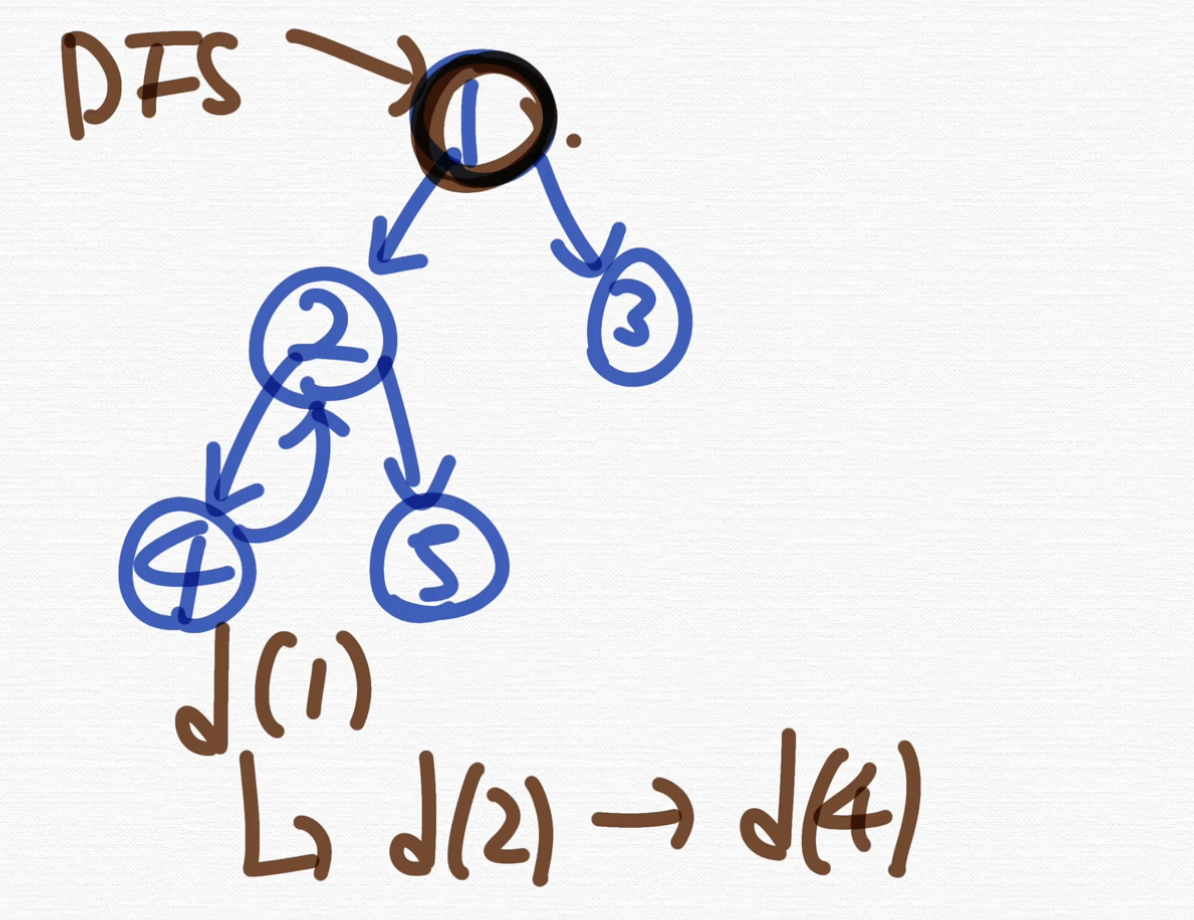
지금 보면 재귀적으로 호출되죠. 호출되는 건 이 순서인데, 종료되는 건 어디서부터 종료돼요? 4부터 종료됩니다.
자, dfs(4)가 여기까지 들아왔다고 칩시다. 그러면 4에 연결된 간선이 2가 있지만 이거는 이미 방문했기 때문에 dfs(4)로부터 다시 어떤 dfs가 호출되지 않아요.

그래서 이렇게 흘러와서 return이 돼버리는 겁니다.
실행을 시켜보면,

이렇게 됩니다. 그래서 이런 식으로 디버깅을 하면서 '아 이게 이때 호출이 되고 이게 이렇게 종료가 되는구나' 라는걸 알 수가 있습니다.
이제 DFS를 구현하는 방법에 대해서 얘기를 해보도록 할게요.
지금까지 했던 것처럼 수도코드를 기반으로 할 수도 있지만 사실은 DFS를 구현하는 방법은 총 두 가지가 있어요. 딱 이 두 가지만 아시면 돼요.
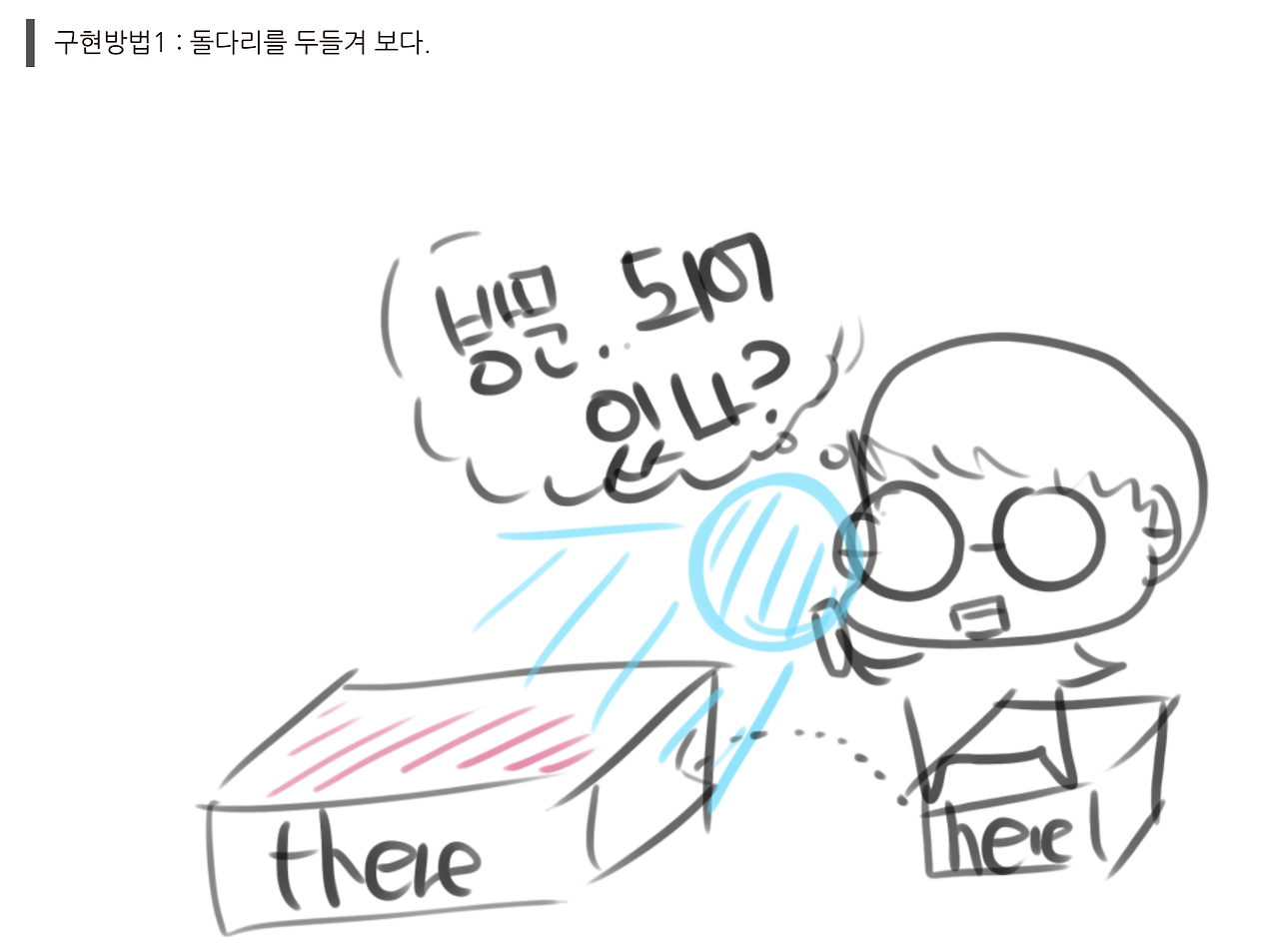
뭐냐면 첫 번째는 돌다리를 두들겨 보는 방법이에요.
그러니까 어떠한 정점에서 어떠한 정점으로 갈 때 방문되어 있나? 라고 확인하고 들어가는 방법인데 바로 이런 방법이에요.

정점을 색칠하고, 그 다음에 이런 식으로 만약에 이 노드가 방문되어 있다면 방문하지 않고 dfs를 호출하는 거에요.

수도코드랑 거의 비슷하죠? 이게 첫번째 방법이고,

두번째는 못먹어도 Go 라는 방법이에요.

이건 뭐냐면 방문했든, 안했든 무조건 Go를 하는거예요.
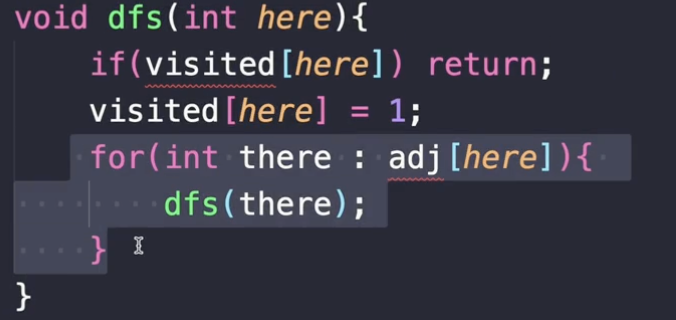
뭐냐면 이거 보시면 수도코드랑 좀 다르죠. 원래는 이 안에서 방문했는지, 안했는지 체크하는 로직이 있었는데 없죠.
얘는 방문했는지 안했는지는 상관없어요. 무조건 함수를 호출하는 거예요. 그리고 함수 초반에 이런 식으로 리턴을 해버려요.
그러니까 수도코드처럼 작성할 수도 있지만 실제로 저희가 알고리즘 문제를 풀다보면 이런 식의 두 가지 방법을 사용하게 돼요.
돌다리를 두들겨 보는 방법, 그리고 못 먹어도 Go 하는 방법. 이 두 개의 코드 모두 자유롭게 구현하실 줄 아셔야 됩니다.
자 문제를 풀면서 조금 더 자세하게 얘기를 해보도록 할게요.



이런 식으로 맵이 주어집니다. 어떻게 답을 구해야 되냐?

이런 문제는 사실 앞에서 설명한 connected component를 찾는 문제죠. 이런 식으로 제가 예제 입력을 이렇게 그림으로 나타낸 거예요.
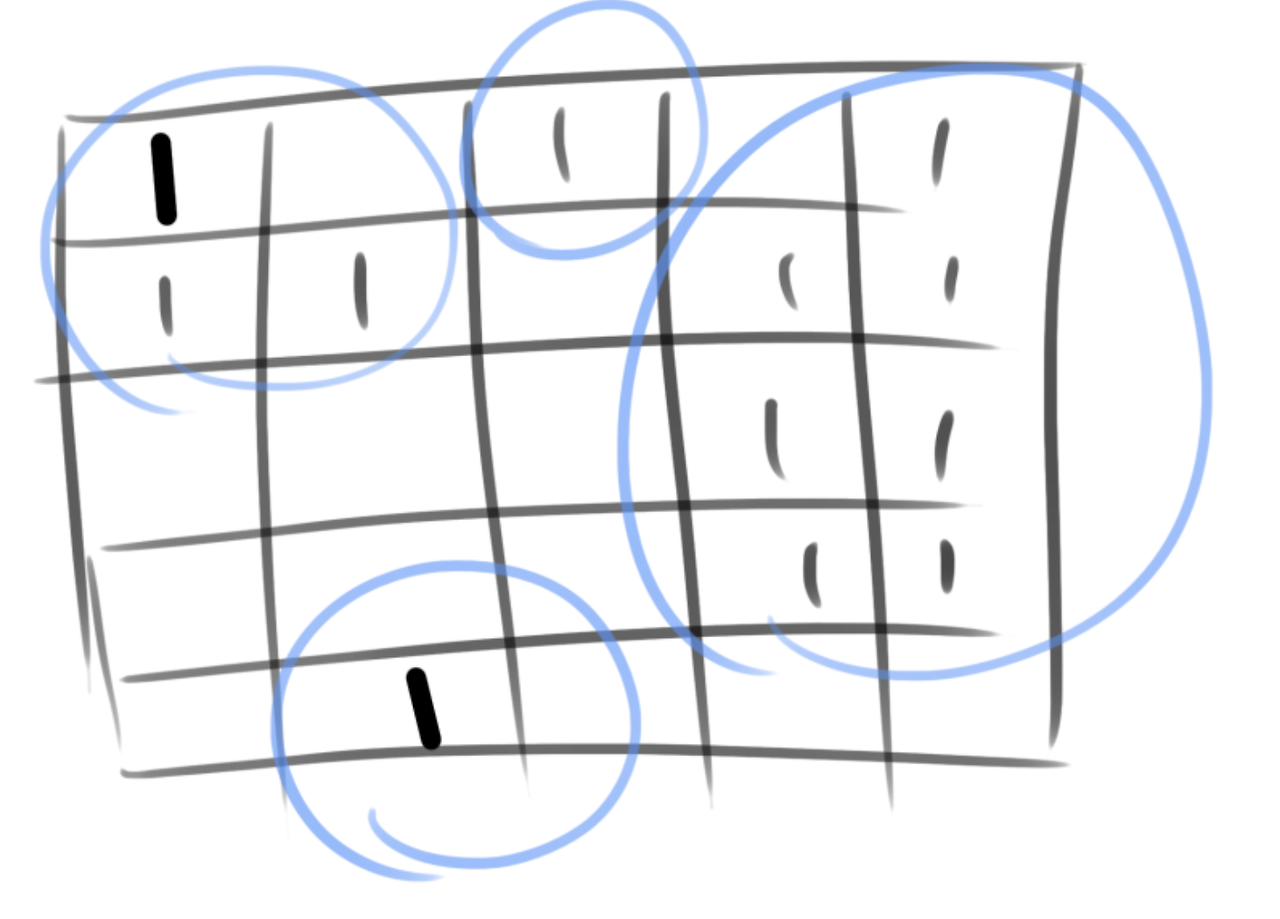
그러면 4번만 방귀를 뀌게 되면 모든 육지, 1로 된 맵을 다 오염시킬 수가 있는 거죠.
여러분 어떤 탐색이나 퍼져나간다 라고 했을 때는 이런 식으로 그래프 탐색, BFS나 DFS 알고리즘을 생각을 하시면 돼요.
그러니까 이 문제 같은 경우는 방귀가 퍼져나가는 거죠. 그러니까 이러한 정점과 정점들이 이렇게 연결되어 있는데 퍼져나간다를 이해하고 구현을 해야 되는 거잖아요.
그렇기 때문에 그래프 탐색 알고리즘인 BFS나 DFS를 생각을 하시면 돼요.
다시 정리하면, 만약에 그래프를 탐색한다, 그래프를 퍼져나간다고 했을 때는 그래프 탐색 알고리즘인 BFS나 DFS를 한 번쯤은 생각을 하셔야 돼요.
정답코드를 기반으로 DFS를 한번 설명을 해보도록 할게요.



자 이 코드는 사실 예전에 했던 코드와 좀 비슷하긴 해요.
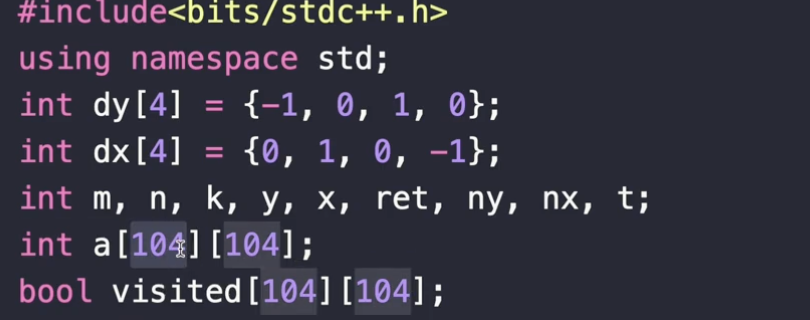
일단 문제의 범위가 100이기 때문에 넓직하게 104로 여유있게 설정한 겁니다.
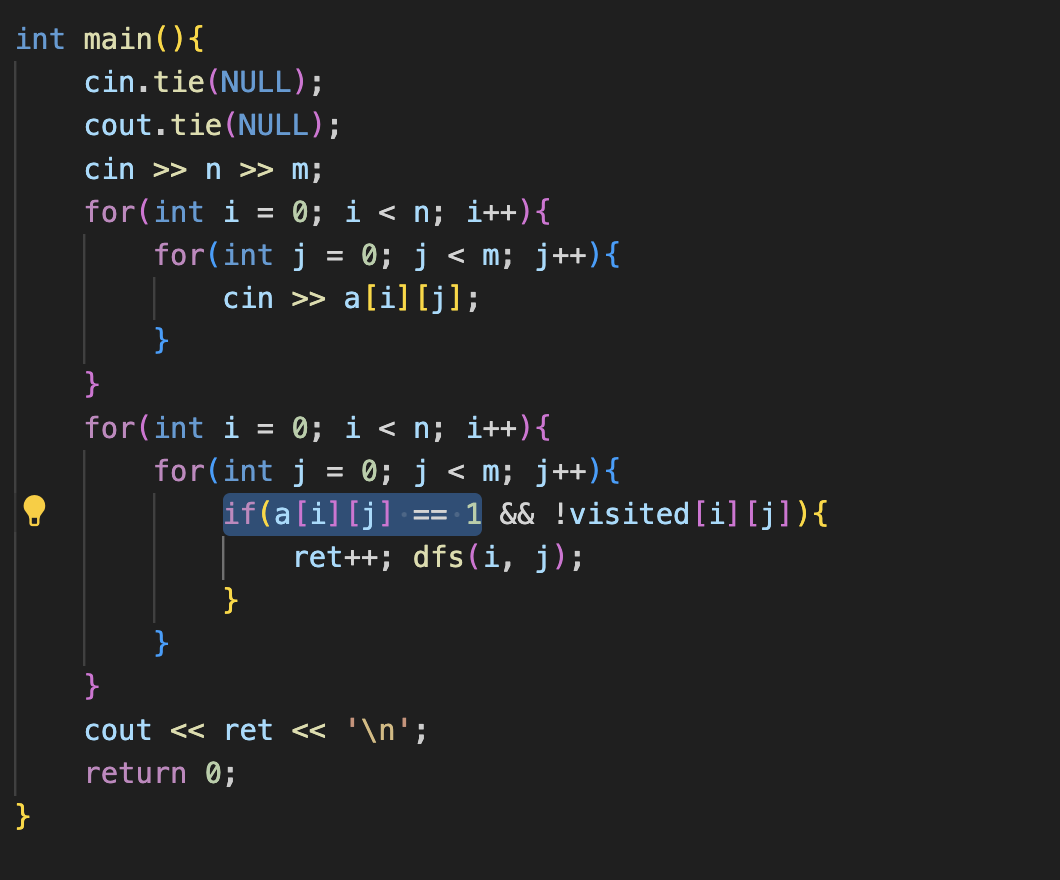
그리고 육지를 먼저 찾죠. 육지를 찾고나서 거기서부터 시작하는 겁니다. 그리고 방문하지 않았다면 이렇게 ret을 ++ 하면서 dfs를 호출 합니다.

dfs를 보면,
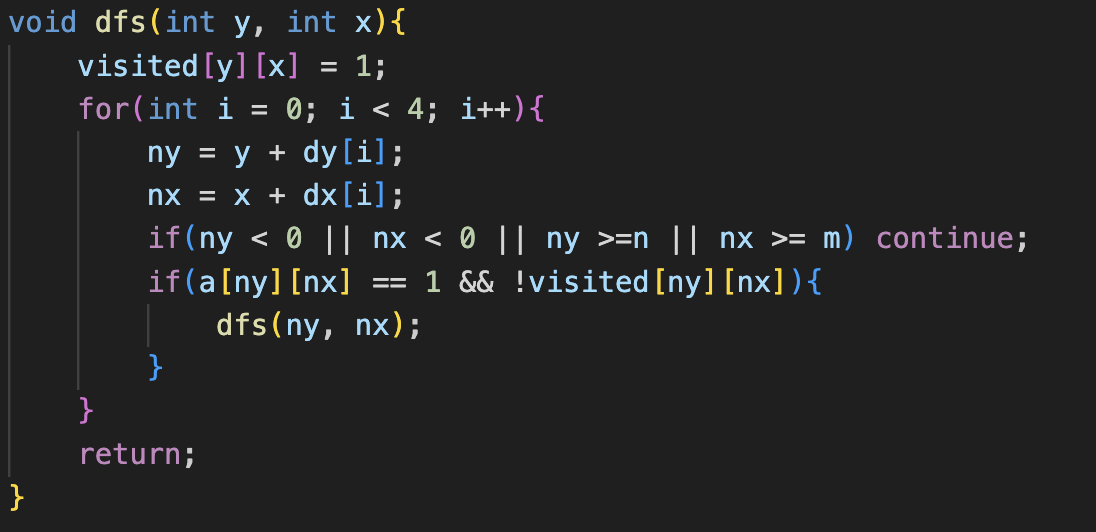
y, x로 시작합니다. 우리가 전에 했던 dfs는 1차원이었죠.
이건 2차원 좌표이기 때문에 이런 식으로 y, x를 매개변수로 하는 dfs를 만든거구요.
이런 식으로 4방향을 탐색하고 ny, nx를 정의하고 그 다음에 overflow, underflow를 체크한 다음, 만약에 방문되어 있지 않다면 dfs를 호출하는 굉장히 쉬운 알고리즘 입니다.

만약 여기서부터 탐색이 일어난다고 하면, 저 한 덩어리에 있는 정점들이 dfs를 통해 호출되고요.
저 한 connected component가 끝나면,

다음 덩어리의 시작을 찾을 때 또 ret++이 되겠죠. 그렇게 해서 총 4개를 출력하게 되는 알고리즘 입니다.
만약에 이해가 잘 안된다고 하면, 디버깅 코드를 작성해서 확인해보세요.


이렇게 디버깅 코드를 작성해서 이해하는 것도 하나의 방법입니다.
제가 한 번 더 강조를 하고 강의를 마치도록 할텐데, 여러분 dfs를 구현하는 방법은 딱 두가지 입니다.
이거를 진짜 자유롭게 구현할 수 있을 줄 알아야 되고 외우셔야 돼요.
첫번째 방법은 돌다리를 보고 구현하는 방법이었죠.

두 번째 방법은 무조건 호출해! 방법입니다.

그리고 이렇게 1차원 배열인 경우와 달리, 2차원 배열인 경우에는 매개변수를 2개 받아서 y, x라는 좌표로부터 nx, ny 정의하는 것까지 얘기를 해봤습니다.
다시, DFS는 그래프를 탐색할 때 쓰는 알고리즘이고 어떤 노드부터 시작해서 인접한 노드들을 재귀적으로 방문하며, 방문한 정점은 다시 방문하지 않으며 각 분기마다 가능한 가장 멀리 있는 노드까지 탐색하는 알고리즘 입니다.
'10주완성 C++ 코딩테스트 | 알고리즘 코딩테스트 > 2주차 : 그래프이론 DFS BFS' 카테고리의 다른 글
| 2주차 개념 #8. 연결된 컴포넌트(connected component) (0) | 2024.03.24 |
|---|---|
| 2주차 개념 #7. 맵과 방향벡터(direction vector) (0) | 2024.03.24 |
| 2주차 개념 #6. 인접행렬과 인접리스트의 차이 (0) | 2024.03.21 |
| 2주차 개념 #5. 인접리스트(adjacency list) (0) | 2024.03.20 |
| 2주차 개념 #4-2. 인접행렬(adjacency matrix) (0) | 2024.03.19 |




