당니의 개발자 스토리
2주차 개념 #6. 인접행렬과 인접리스트의 차이 본문
2주차 개념 #6. 인접행렬과 인접리스트의 차이
clainy 2024. 3. 21. 22:542주차 개념 #6. 인접행렬과 인접리스트의 차이
저희가 지금까지 인접행렬과 인접리스트를 배워봤어요. 그러면 이 둘 중에 뭘 써야 될까? 그 차이를 배워보도록 하겠습니다.

첫번째는 공간 복잡도예요.

인접행렬은 O(V^2), 인접 리스트는 O(V + E)만큼이 필요하다는 거예요. V는 vertex, E는 edge라고 했죠.
여러분 인접행렬은 뭐라고 했죠? 인접행렬은 단순무식하게 vertex가 만약에 100개라면 100개씩 이렇게 2차원 배열을 만든다 라고 했죠.

이게 인접 행렬이에요. 그렇기 때문에 인접 행렬의 공간 복잡도는 O(V^2)이 필요한거죠.
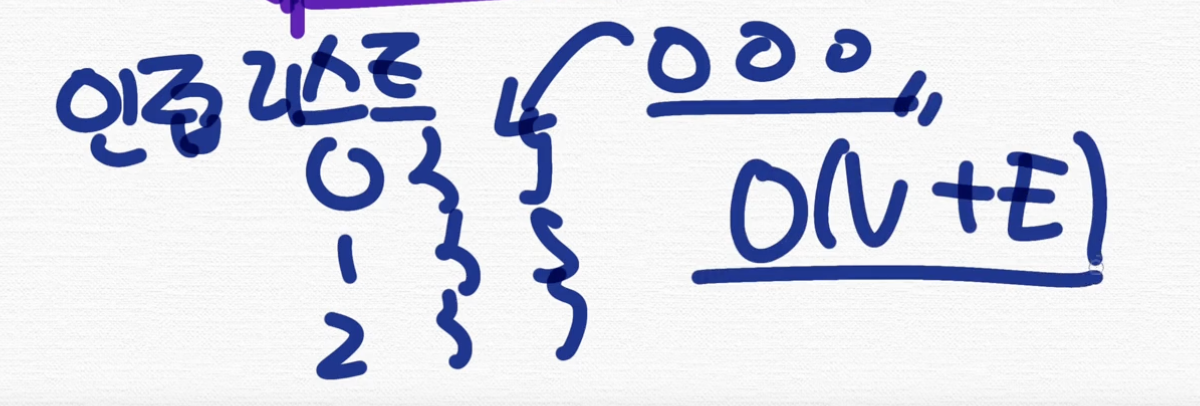
'아니 근데 선생님 인접 리스트는 각 정점마다 연결 리스트를 만들어서 정점을 집어넣는다 라고 한거 아닌가요? 인접행렬이 O(V)까지는 이해를 하겠는데, 인접 리스트는 왜 플러스 E(edge)가 들어가나요?'
여러분 인접 리스트만 생각을 해볼게요. 인접 리스트는 연결된 정점만 연결 리스트에 들어가죠? 그러니까 정점이 여러 개가 있더라도 연결된 정점만 들어가기 때문에,

즉 정점마다 이 정점과 연결된 간선의 개수 만큼만 들어가는 거라서 + E가 필요한 거예요.

지금 보시면 연결되지 않은 정점들 안 들어가잖아요. 그래서 O(V + E)가 됩니다.
두 번째는 시간 복잡도인데요.

시간 복잡도는 간선 1개 찾기와 모든 간선 찾기가 있습니다.
예를 들어서 어떤 i에서 j까지 가는 간선이 있냐, 없냐를 찾는 것은 인접행렬은 O(1)이에요. 그냥 a[i][j] 값이 있는지만 보면 되잖아요.

이렇게 for문을 사용해서 간단하게 확인할 수가 있죠. 정말 단순무식하게 2차원 배열을 만들어놨으니까.
근데 인접리스트는 O(V) 예요.

인접 리스트는 어떠한 정점마다 연결 리스트를 만들고 이 연결 리스트에다가 0, 1, 2 이렇게 연결된 정점을 집어넣는다고 했죠.

그러니까 i에서 j까지 가는 간선이 있냐고 했을 때 그 연결 리스트에 들어가서 j 라는 값이 있는지 하나씩 탐색해봐야 되는 거잖아요.
인접 행렬에선 a[i][j]에서의 j는 to 정점이었는데, 인접 리스트에서의 j는 to의 의미가 아니라 그저 인덱스죠.

아까 설명을 했는데 이렇게 연결된 정점들만 집어넣기 때문에 간선의 개수만큼 확인을 하니까 O(E)가 아닌가요? 라고 할 수가 있어요.
그런데 지금 우리는 최악의 시간복잡도예요.
그러니까 사실은 시간복잡도를 판단할 때 평균적인 시간복잡도와 최악의 순간의 시간복잡도, 이 두 가지를 판단하는데 보통은 이 두 가지 중에서도 최악의 시간복잡도를 많이 써요. 그래서 최악의 경우를 따져볼까요?

최악의 경우는 인접 리스트가 모든 정점과 연결되어 있는 경우죠. 그래서 이 경우에는 O(E)보다 O(V)가 나은 표현이겠죠.
그러니까 다시 정리를 하자면,
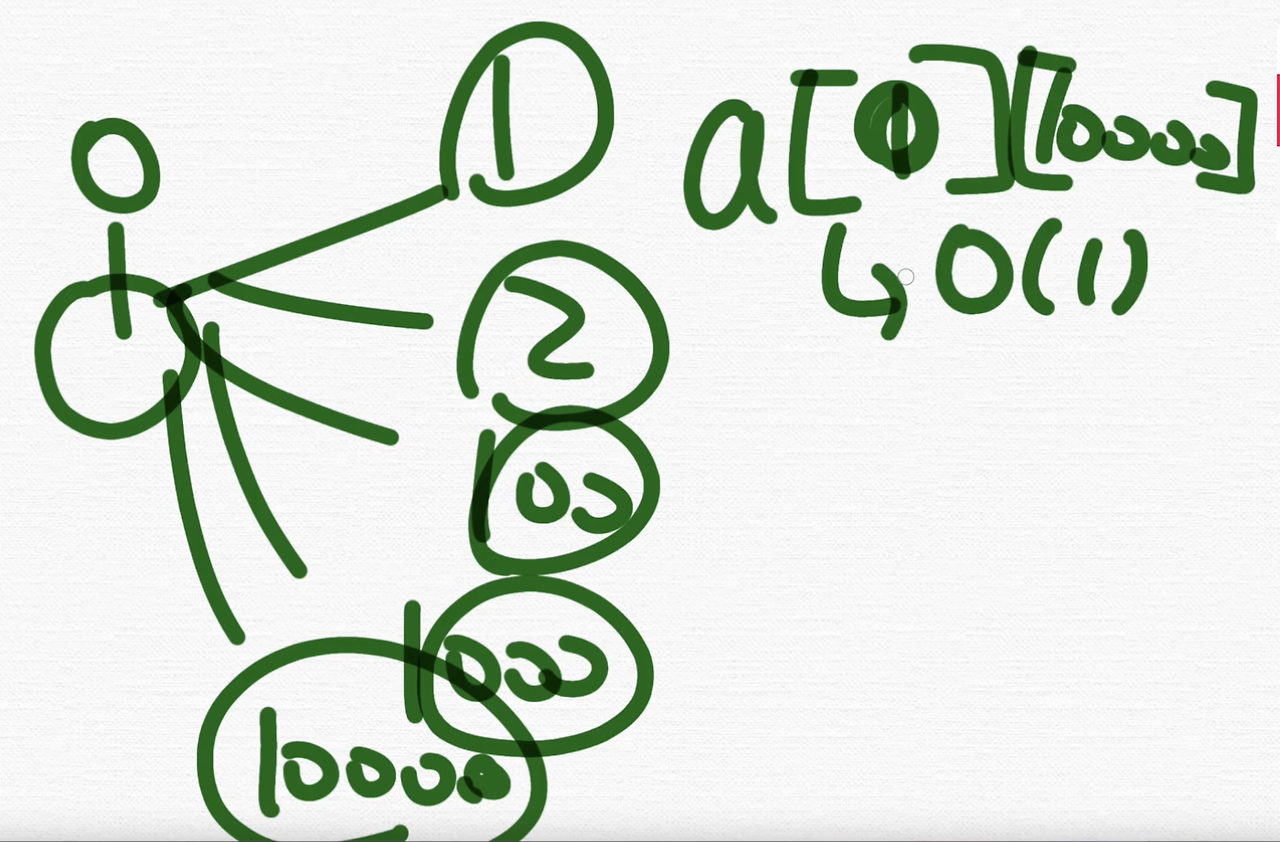
만약에 이렇게 정점이 연결되어있을 때, 0번과 10000번이 연결되어있는지 보려면, 인접행렬은 a[0][10000] 이렇게 하면 확인 끝이죠. 이게 O(1)이라는 거예요.

근데 인접 리스트는 for문을 통해서 연결된 거를 전부다 확인해봐야 되는 거예요. 그래서 O(V) 입니다.
이제 모든 간선 찾기를 봅시다.

인접행렬은 2차원 배열을 다 순회를 해야 되니까 O(V^2) 이고요. 인접 리스트는 O(V + E) 입니다. 왜냐하면 이만큼 공간을 가지고 만들었기 때문에 전체적으로 탐색하는 것 자체도 공간복잡도만큼 걸린다는 겁니다.
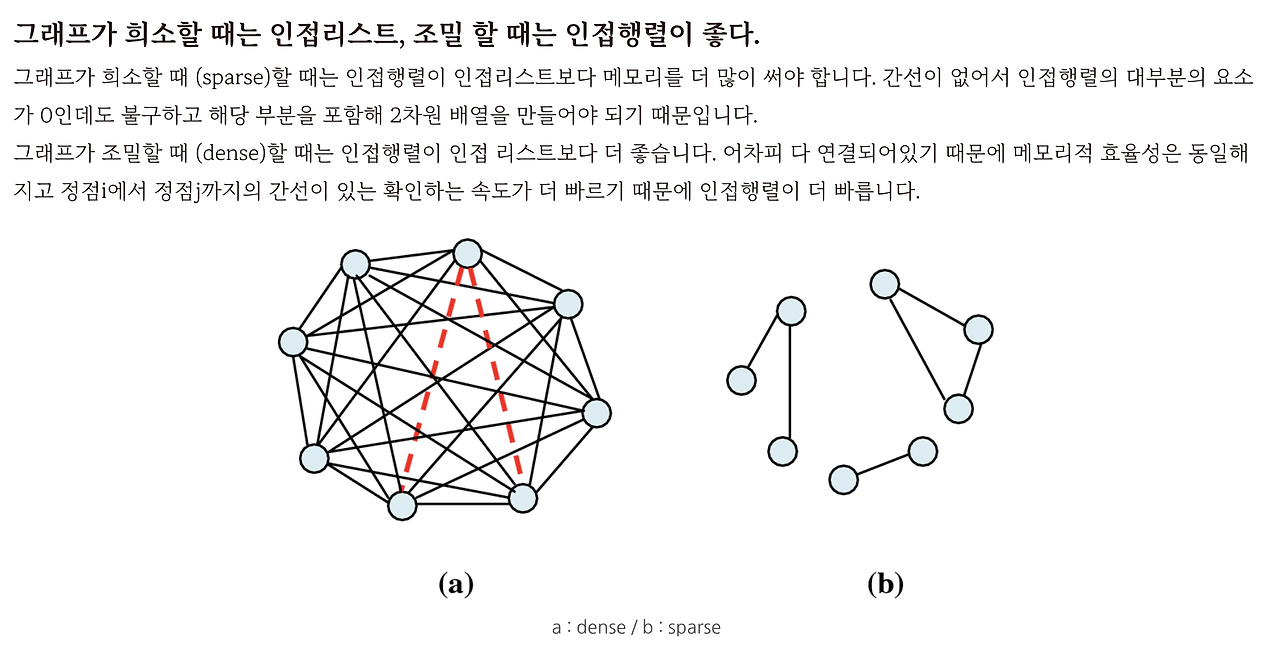
또 하나가 있는데, 그래프가 희소할 때는 인접 리스트가 좋고, 그래프가 조밀할 때는 인접 행렬이 좋아요.
그래프가 희소하다 라는 것은 sparse 하다. 라고 해요. 그래서 sparse 할 때는 인접행렬이 인접리스트보다 메모리를 더 많이 써야돼요.
그러니까 인접행렬은 제가 무식하게 2차원 배열을 만든다 라고 했죠.

근데 예를 들어서 이렇게 되어 있는 그래프가 있다라고 쳐요. 얘네들은 연결이 안 되어있잖아요 서로. 그런데 연결이 되어있지 않음에도 불구하고 2차원 배열을 다 만들어야 된다라는 거예요. 그래서 이때는 인접행렬이 인접리스트보다 메모리를 더 써요.
그런데 인접 리스트는 연결된 정점만 집어넣는다고 했죠. 연결된 정점 자체가 별로 없을 때, 즉 sparse 할 때는 연결된 정점만 집어넣는 인접 리스트를 쓰는 게 더 빠르고 좋다는 거예요.
그래프가 조밀할 때 (dense)할 때는 인접행렬이 인접 리스트보다 더 좋아요. 간선들이 많은 게 dense 한 거예요. 왜냐하면 어차피 이렇게 조밀하니까 메모리적 효율성은 동일할 거 아니에요. 어차피 다 연결되어있기 때문에 메모리적 효율성은 동일해지고 정점 i에서 정점 j까지의 간선이 있는지 확인하는 속도가 더 빠르기 때문에 인접행렬이 더 빠릅니다.
그래서 그래프가 희소할 때 (sparse)할 때는 인접 리스트, 조밀할 때 (dense)할 때는 인접행렬을 쓰면 됩니다.
그러면 결과론적으로 뭘 쓰면 좋을까?

여러분 보통은 인접 리스트를 쓰시면 돼요. 왜냐하면 알고리즘 문제나 코딩 인터뷰에서 주어지는 문제를 보면 sparse 한 그래프가 많이 나와요. 모든 간선이 연결되어있는 dense 한 그래프는 자주 나오지가 않습니다.
경험에서 나오는 짬밥으로 여러분들한테 알려준다 라고 생각을 하시면 돼요. 100% 맞는 얘기는 아니예요.
지금 보시는 것처럼 그냥 일단은 인접리스트를 써보고 다만 문제 또는 코딩 인터뷰에서 인접행렬로 주어지잖아요. 그러면 그냥 그때는 인접행렬로 푸는 게 좋은데 보통은 일단 인접리스트를 쓸 생각을 하셔야 돼요. 왜 그러냐면 제 경험에서 나온 짬밥을 통해서 알려드릴게요.
여러분 보통은 인접 리스트를 쓰시면 돼요. 왜냐하면 알고리즘 문제나 코딩 인터뷰에서 주어지는 문제를 보면 sparse 한 그래프가 많이 나와요. 모든 간선이 연결되어있는 dense 한 그래프는 자주 나오지가 않습니다.
경험에서 나오는 짬밥으로 여러분들한테 알려준다 라고 생각을 하시면 돼요. 100% 맞는 얘기는 아니예요.
지금 보시는 것처럼 그냥 일단은 인접리스트를 써보고 다만 문제 또는 코딩 인터뷰에서 인접행렬로 주어지잖아요. 그러면 그냥 그때는 인접행렬로 푸는 게 좋은데 보통은 일단 인접리스트를 쓸 생각을 하셔야 돼요. 왜 그러냐면 제 경험에서 나온 짬밥을 통해서 알려드릴게요.
뭐냐면 우리가 코딩 테스트를 본다고 쳐요. 코딩 인터뷰도 마찬가지예요.

이런 식으로 문제가 예제 입력과 예제 출력 이렇게 문제와 예제가 주어지잖아요.

이런 공개적으로 나타낸 테스트 케이스를 Public TC라고 해요. TC는 테스트 케이스의 약자입니다.
그래서 예제를 맞았다고 하면 여러분들이 이 코드를 제출하게 되죠.

제출하게 되면 이 문제를 푸는 사이트 안에 있는 Private한 테스트 케이스를 통과하는지를 확인해요. 그래서 만약에 통과를 했다고 치면은 맞았다고 뜨는 거예요. 이 테스트 케이스 누가 만드는지 아세요? 사람이 만듭니다.
근데 dense한 그래프를 만드는 것들이 사람이 만들기에는 조금 복잡하고 어려워요.
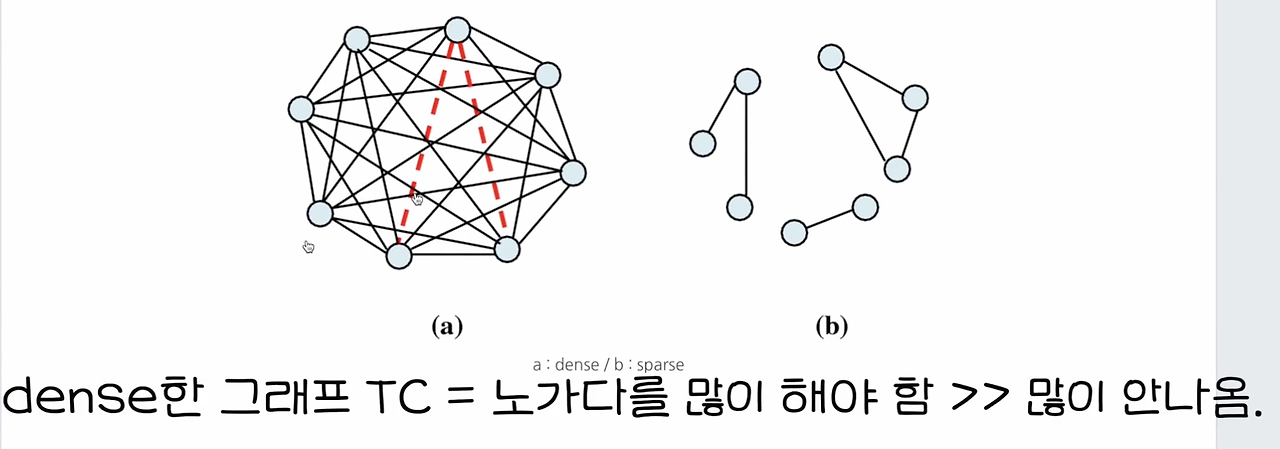
그래서 대부분의 문제들이 보통은 이런 sparse한 그래프로 주어지는 경우가 많다는 거예요.
다시 인접행렬과 인접리스트의 차이는 공간 복잡도와 시간 복잡도 차이에 있다는 것을 꼭 외워주고 있어야 돼요. 이거는 면접에서도 많이 나오고 코테에서도 많이 나오니까. 근데 만약에 알고리즘 문제를 푼다고 했을 때 보통은 인접리스트를 쓸 생각을 하시고요.
만약에 문제 또는 코딩 인터뷰에서 인접행렬로 주어진다 라고 하면 그대로 인접행렬로 푸시는 게 좋다라는 겁니다.
'10주완성 C++ 코딩테스트 | 알고리즘 코딩테스트 > 2주차 : 그래프이론 DFS BFS' 카테고리의 다른 글
| 2주차 개념 #8. 연결된 컴포넌트(connected component) (0) | 2024.03.24 |
|---|---|
| 2주차 개념 #7. 맵과 방향벡터(direction vector) (0) | 2024.03.24 |
| 2주차 개념 #5. 인접리스트(adjacency list) (0) | 2024.03.20 |
| 2주차 개념 #4-2. 인접행렬(adjacency matrix) (0) | 2024.03.19 |
| 2주차 개념 #4-1. 인접행렬(adjacency matrix) (0) | 2024.03.19 |




