당니의 개발자 스토리
2주차 개념 #7. 맵과 방향벡터(direction vector) 본문
2주차 개념 #7. 맵과 방향벡터(direction vector)
clainy 2024. 3. 24. 17:532주차 개념 #7. 맵과 방향벡터(direction vector)
우리가 지금까지 그래프라는 걸 표현한다고 했을 때 인접행렬과 인접리스트 라는 걸 배웠죠.

사실은 그래프를 표현한다고 했을 때 이 두 가지 밖에 없어요.

근데 문제에서 이런 것들이 아니라, Map으로 주어지는 경우가 있거든요.

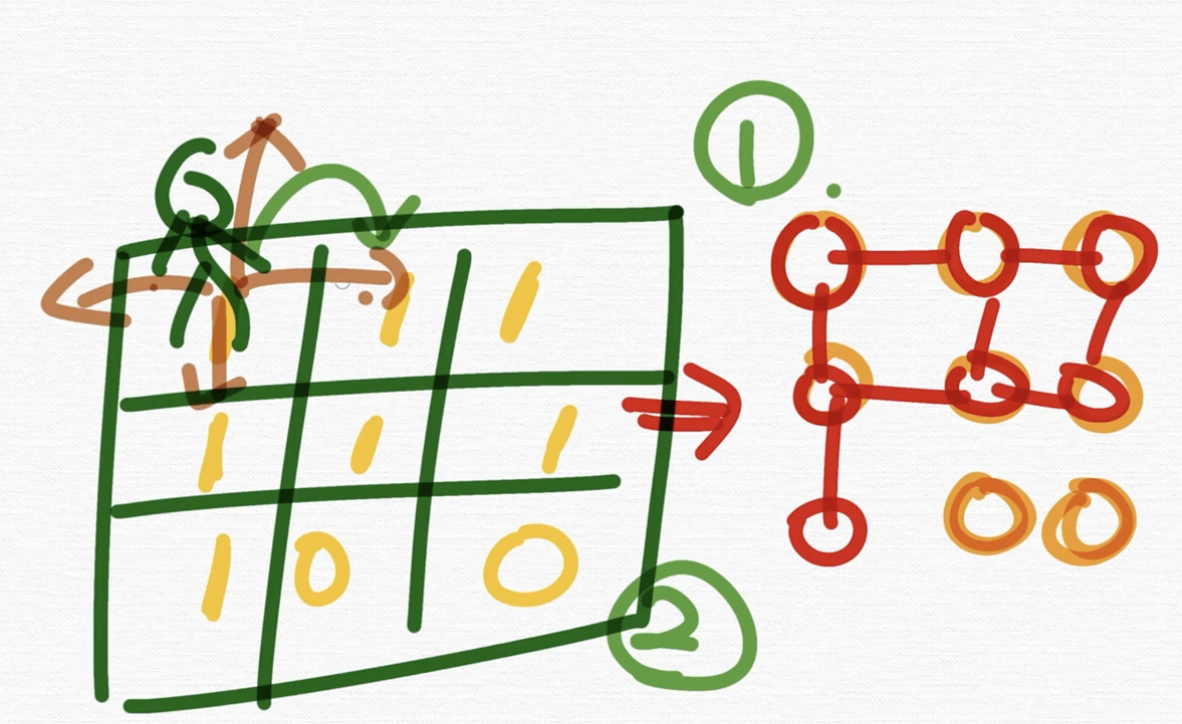
이런 식으로 N 곱하기 M 크기의 배열로 표현되는 미로가 있다. 이렇게 맵으로 주어지는 경우가 있어요. 이 경우에 어떻게 해야 되는지를 얘기를 해보고자 합니다.

뭐냐면 주인공이 이 좌표에 있어요. 이 Map은 1과 0으로 이루어진 지도예요. 여기서 1은 갈 수 있는 곳이고 0은 갈 수 없는 곳이에요.
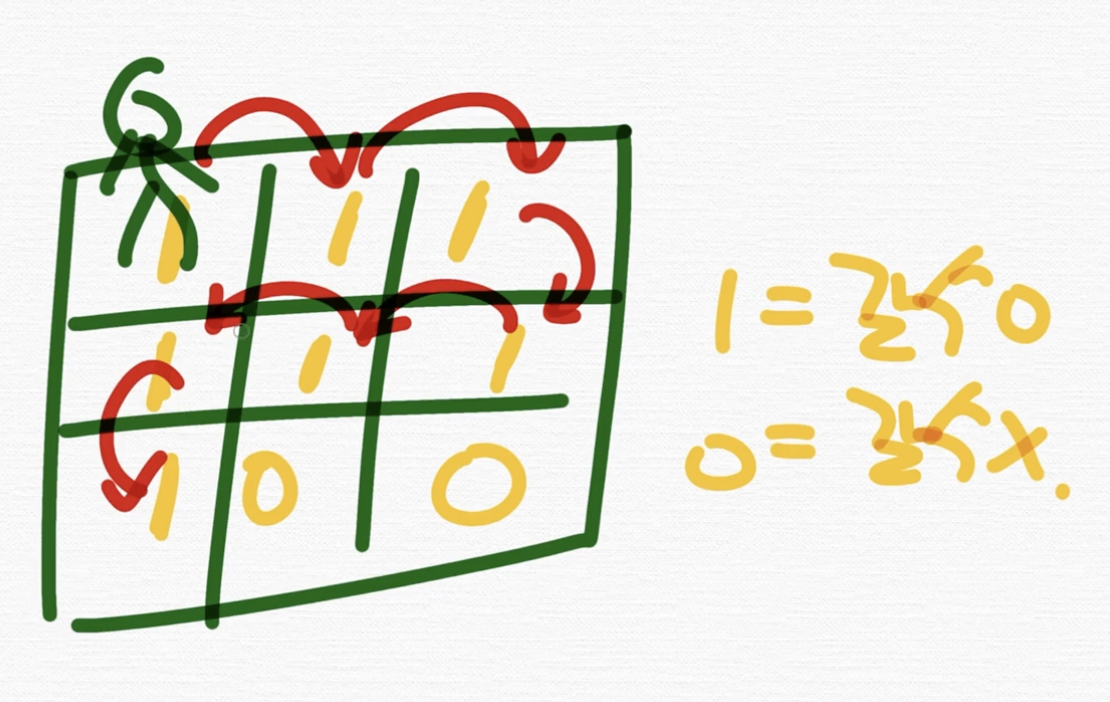
문제에서 주인공은 한 칸씩 이동할 수가 있대요. 그래서 '주인공이 갈 수 있는 모든 좌표를 출력하라' 이런 문제가 있다라고 칩시다.
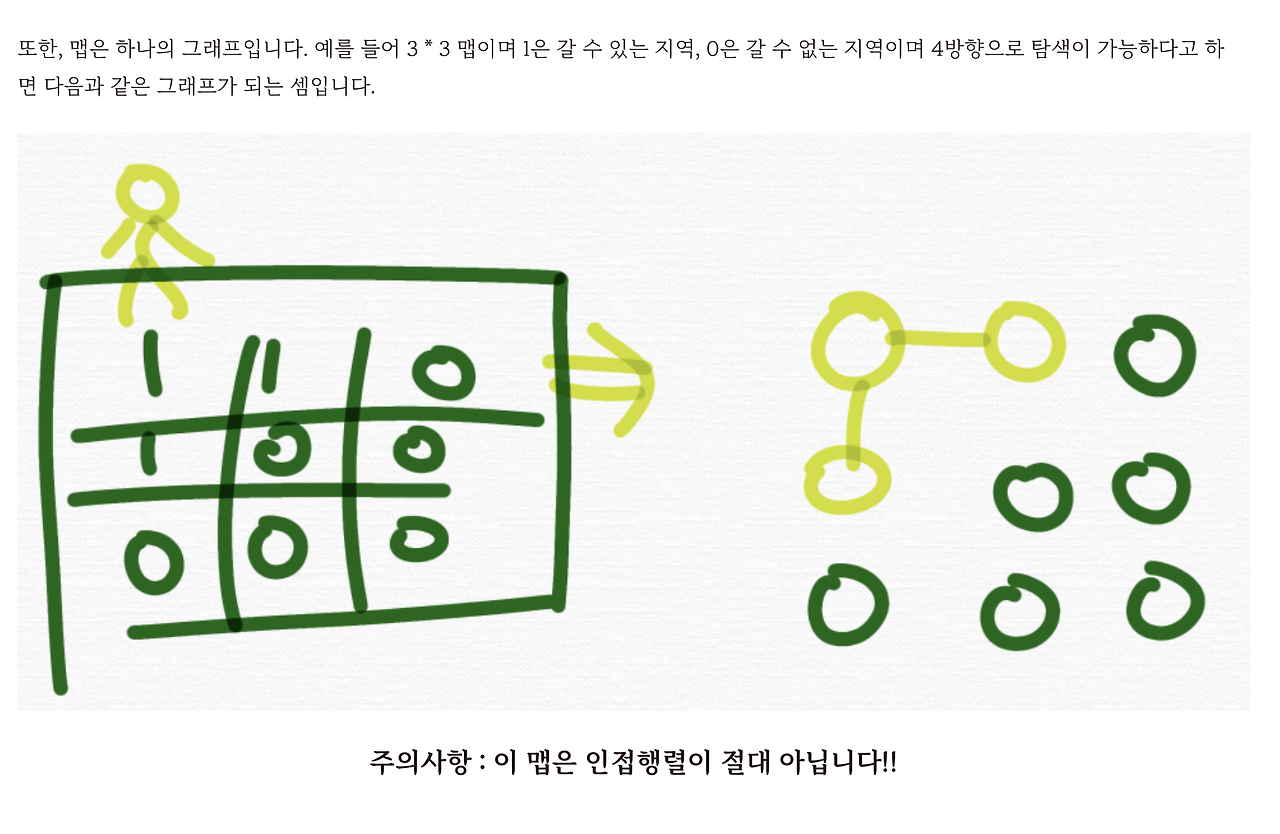
그러면 어떻게 해야 될까요?

우리가 이런 지도를 기반으로 푼다고 했을 때 이 지도를 보고

이런 식의 그래프가 생각이 나야 돼요.
1은 연결이 되어있는 거죠. 정점과 정점으로 연결이 되어있는 거고 지금 보시면은 1은 갈 수 있다 라고 했고 0은 갈 수 없다 라고 했죠. 그래서 이런 그래프를 생각을 하시면 돼요.
여러분들이 '아 갈 수 있는 지점은 이렇게 연결되는 정점들이고, 갈 수 없는 것들은 연결되지 않은 정점이구나' 라고 생각을 하시면 돼요.

다만 지금 보시면 주인공이 한 칸씩 갈 수 있다라고 했죠. 그래서 이러한 간선은 없다는 거예요. 만약에 주인공이 100칸씩도 가능하다. 그럼 이런 간선이 생기겠죠.
근데 한 칸씩 갈 수 있다고 했으니까 이런 그래프를 여러분들이 생각을 하셔야 되는 겁니다.
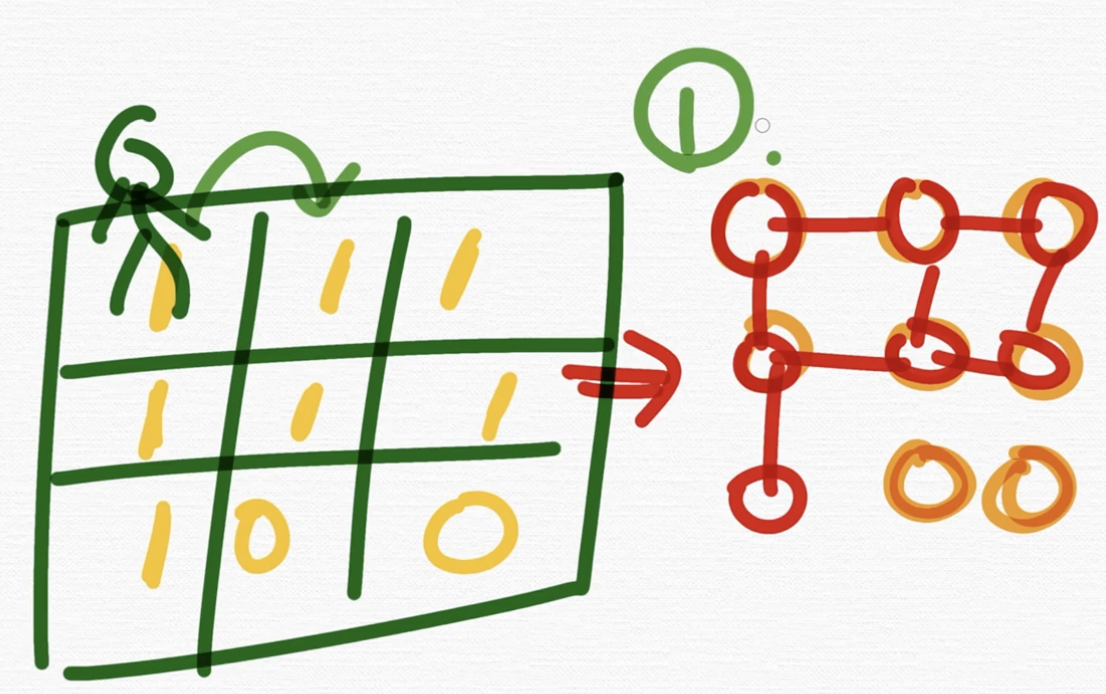
일단은 첫 번째 여기까지 왔어요. 여러분 문제에서 지도 기반으로 주어진다고 했을 때 지도 기반으로 푸셔야 돼요.
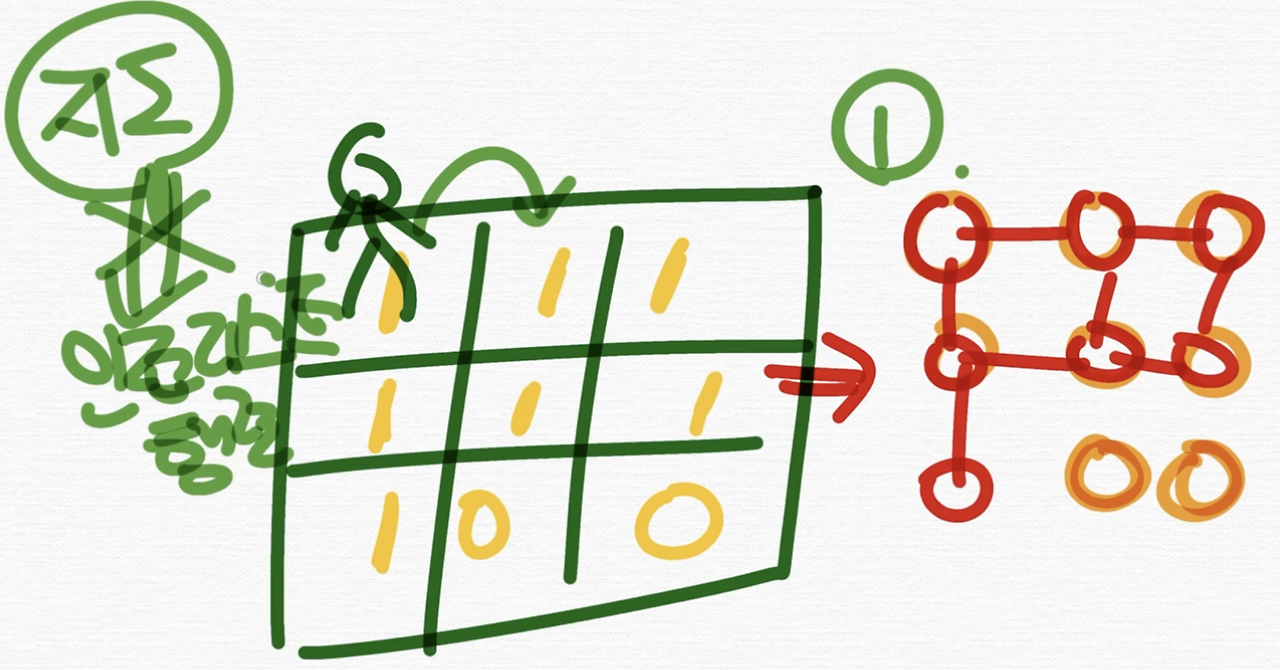
그러니까 지도를 갑자기 인접 리스트나 인접 행렬이나 이런 거로 바꿔서 푸시면 안돼요. 그냥 그 지도 기반으로 푸셔야 돼요.
그걸 제가 오늘 여러분들께 알려드릴 거고요.
그래서 첫 번째가 이 지도를 보고 이런 식으로 정점과 정점 간에 이렇게 연결이 되어 있구나라는 거를 생각하는 거고, 두 번째는 뭐가 필요하냐?
보통 100%는 아니긴 해도 문제에서 4 방향을 탐색하게 하거든요. 상하좌우 이런식으로.
'그러면 어떻게 어떤 좌표에서 4방향을 탐색할 것인가' 라는 게 필요한 거에요. 그러니까 제가 지금 문제를 보고 필요한 로직이나 생각을 얘기를 하는거에요. 첫번째는 지도를 보고 이렇게 인식하는거,

두번째는 이렇게 탐색하는 로직이 필요하고
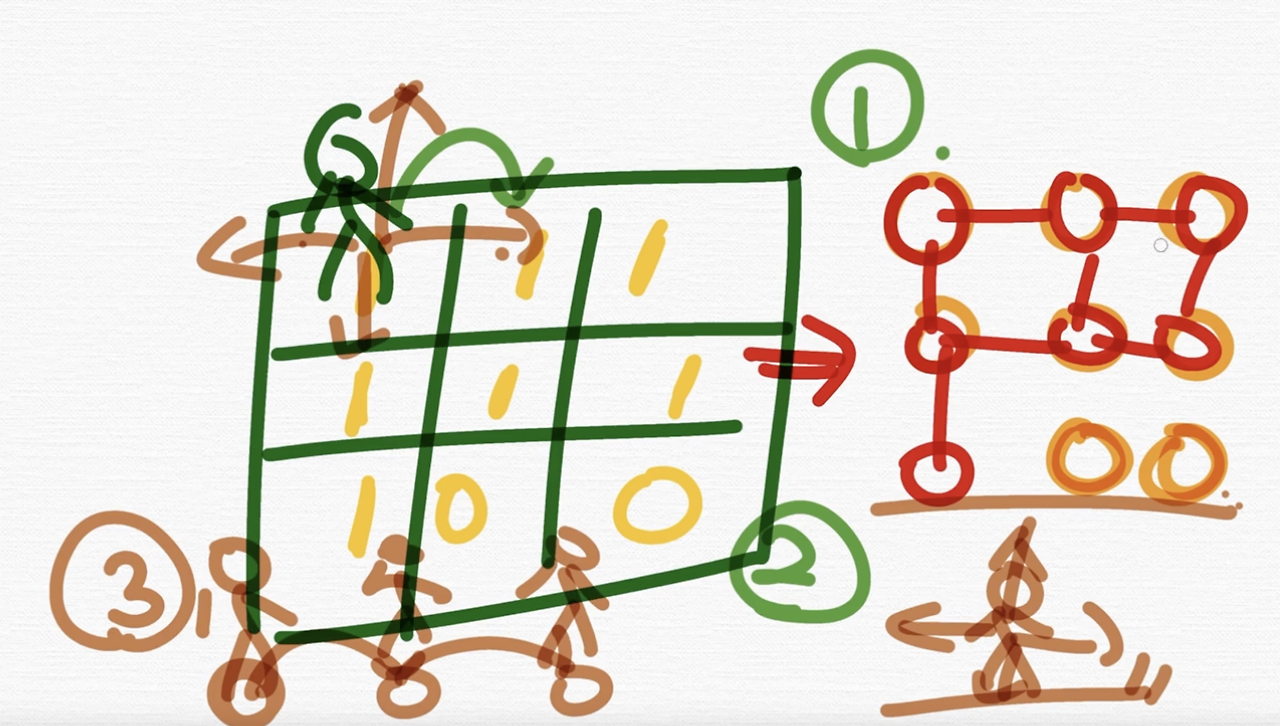
세번째는 만약 이제 여기까지 왔을때, 어떤 정점에서 이렇게 재귀적으로 가는 로직이 필요합니다.
3번은 여러분들이 지금까지 인접리스트나 인접행렬을 풀어보면서 재귀적으로 함수를 만들어서 했어요. 자 문제가 되는 거는 2번입니다.
이렇게 어떤 좌표에서 상하좌우로 탐색하는 거만 알면 사실은 충분히 할 수가 있어요.

자 그러면 2번에 대해서 조금 더 딥하게 얘기를 해보도록 하겠습니다.
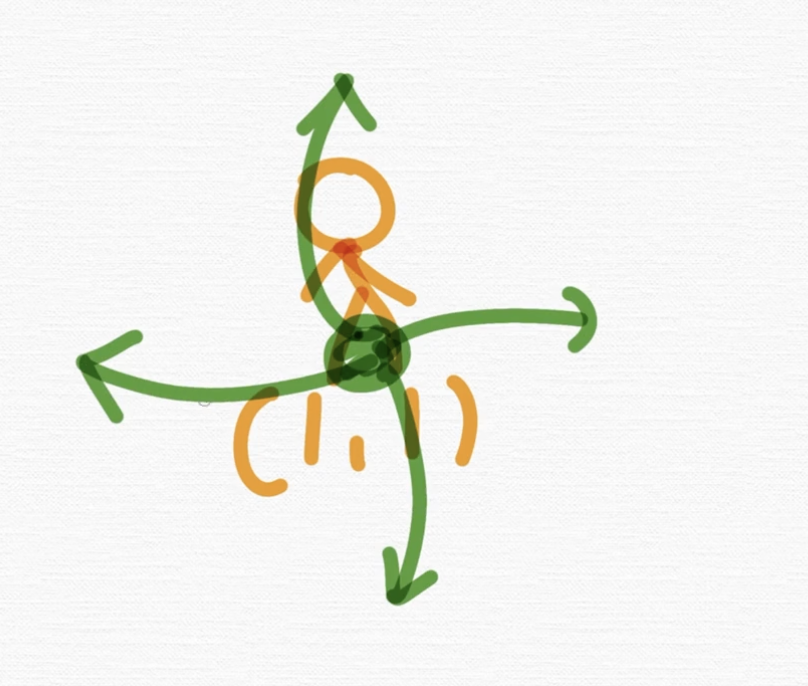
자 위, 오른쪽, 아래, 왼쪽이죠? 이렇게 제가 탐색한다고 해볼게요.

그리고 좌표는 지금 보시면은 제가 이거를 (y, x) 라고 할 거에요. 이게 어떤 분들은 (x, y) 좌표를 기반으로 하시는 분들도 있더라구요.
취향 따라 하는데 저는 (y, x)를 기반으로 합니다. 여러분들도 정말 (x, y)로 해야 되는 엄청난 이유가 없다면 그냥 지금부터는 (y, x)를 기반으로 해주세요.

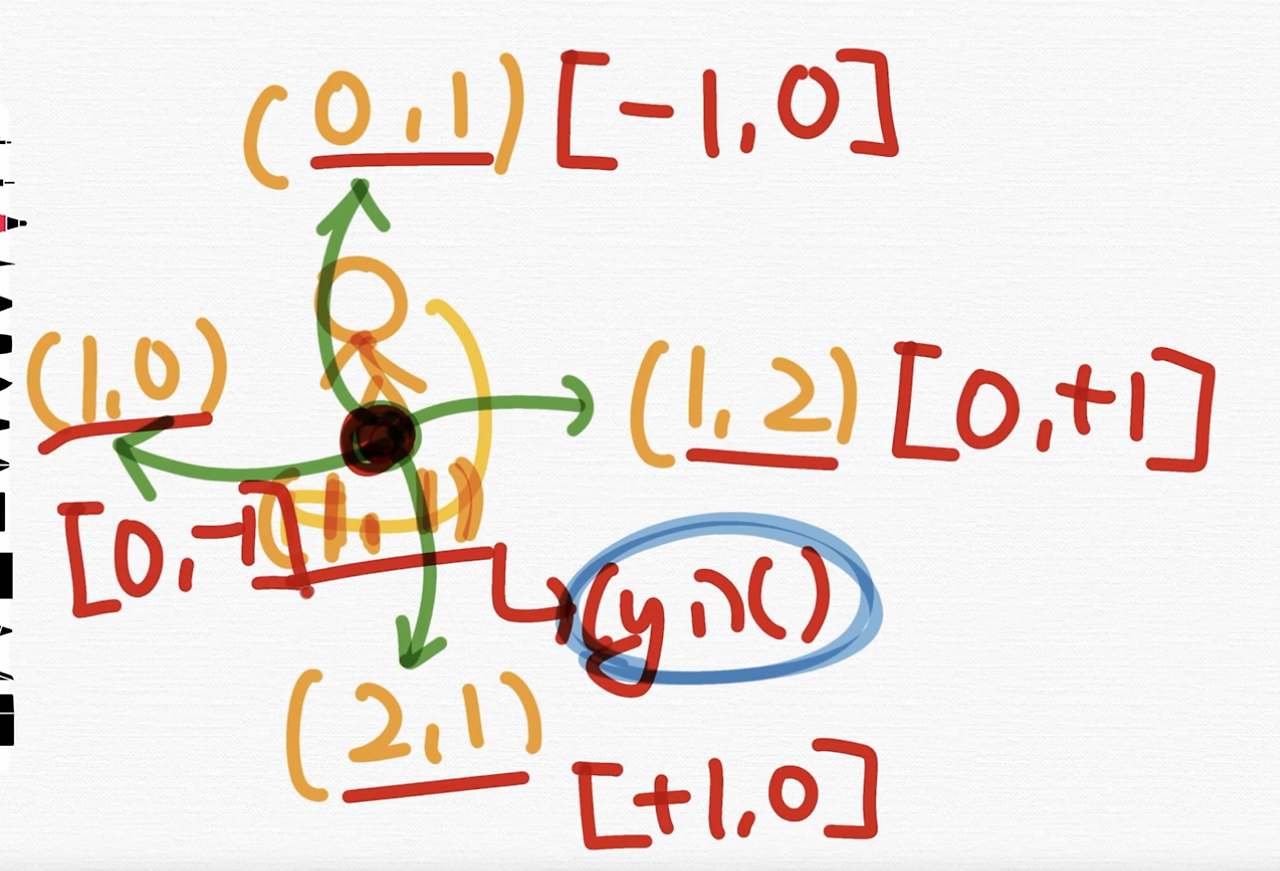
(1,1)에서 위로 간다고 해볼게요. 그럼 어떤 좌표가 돼요? (0,1)이죠.

이런 식으로 할 수 있습니다. y축, x축이니까 실제 좌표평면 상에서는 오른쪽으로 누운 x축, y축으로 볼 수 있는거죠.
지금 여기서 (1, 1)이라는 좌표가 변환된 거잖아요. 변환될 때 변함의 정도만 볼까요? 말이 어렵죠. 그러니까 얼마만큼 이 좌표에서 플러스가 됐냐라는 것만 생각해 볼까요?
여기까지 했어요.
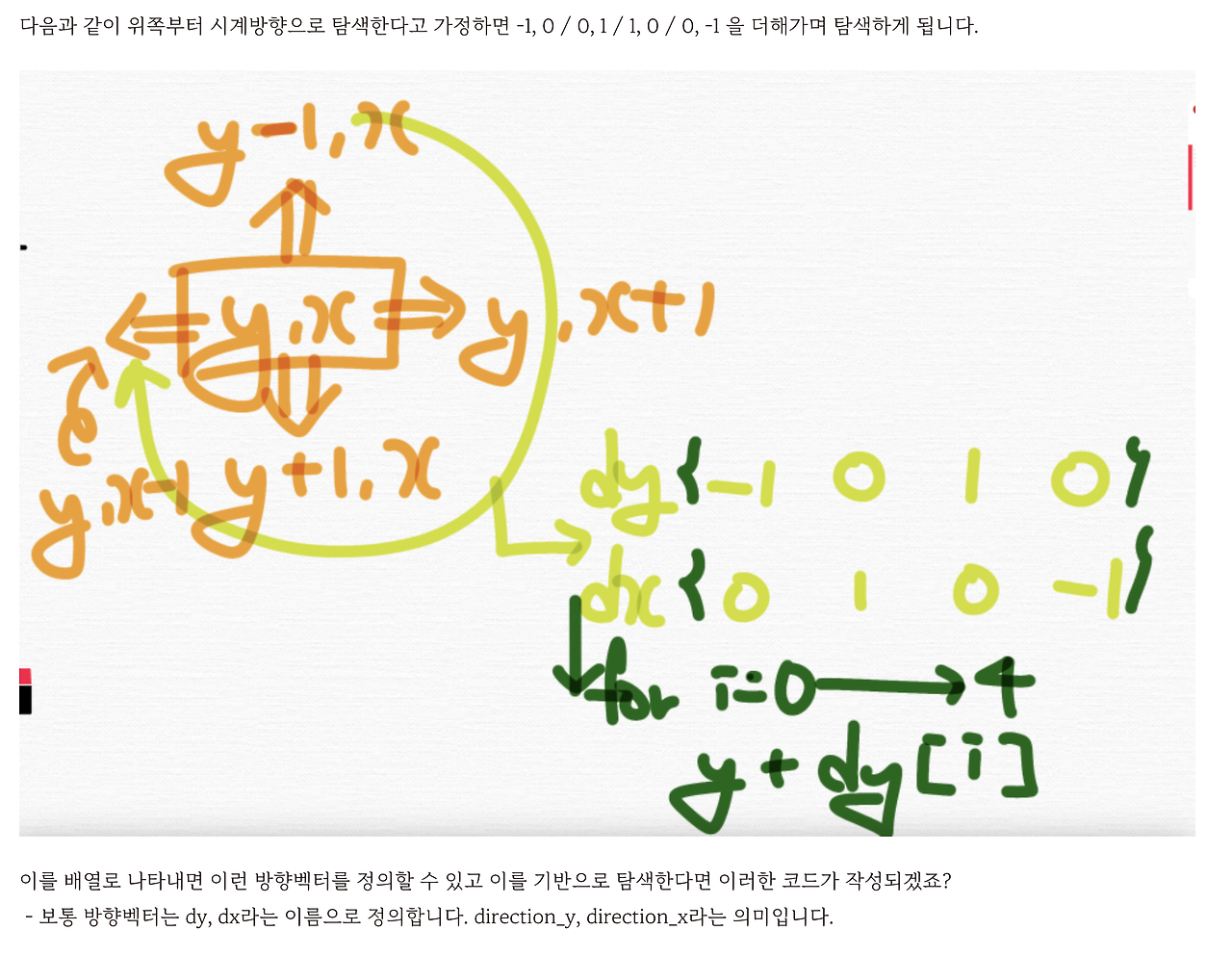
자, 그러면 우리 (y, x) 이렇게 시계방향으로 위부터 위, 오른쪽, 아래, 왼쪽 이렇게 해서 변함의 정도를 나열해 볼까요?

일단 만든 거예요. dy, dx 라는 이름의 배열을 만든거죠.

이런 배열을 만들었죠.

왜냐면 각각 위, 오른쪽, 아래, 왼쪽이었어요.
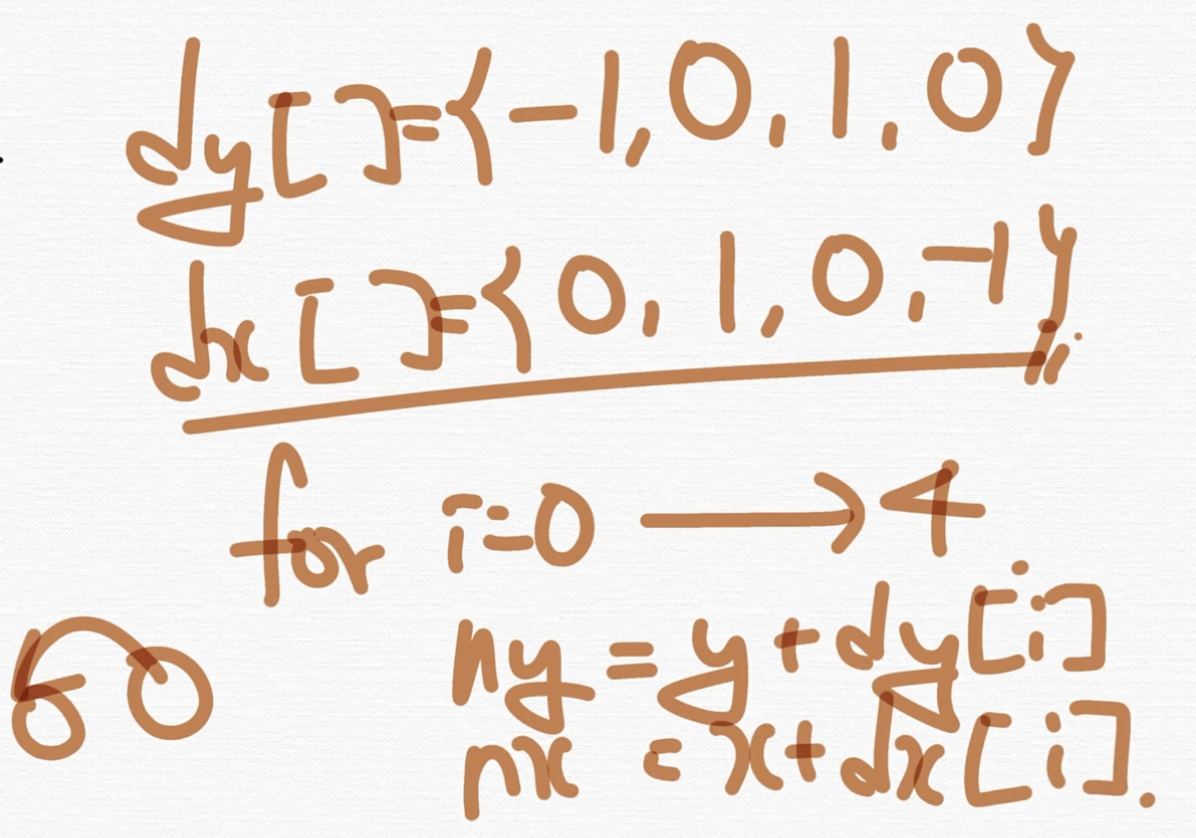
이걸 기반으로 어차피 4방향을 탐색해야 되니까 일단 for 문을 생각할 수가 있겠죠. i = 0부터 i = 4 전까지, 그리고 ny, nx를 정의하는 거예요. 내가 탐색해야 되는 정점, 그니까 이 정점에서 이렇게 움직이는 거니까 ny, nx를 이렇게 정의할 겁니다.
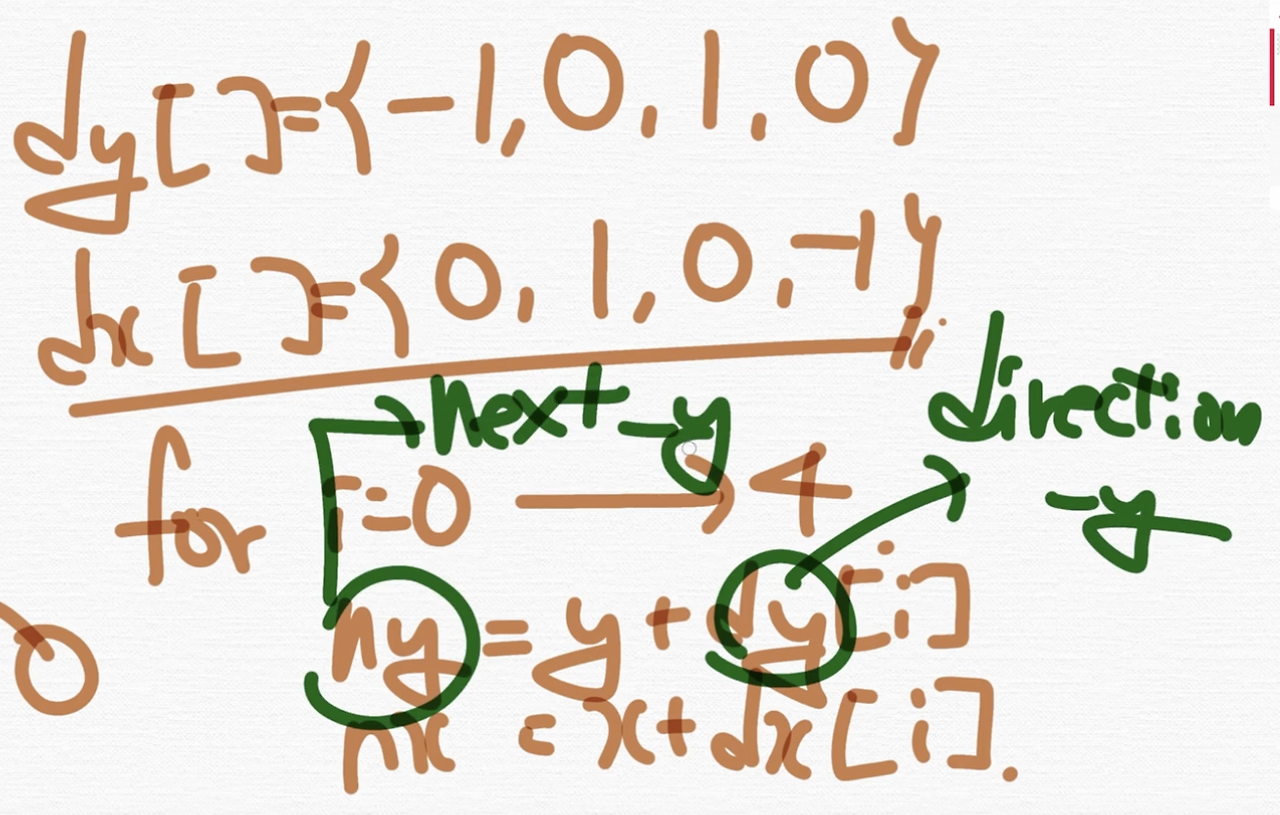
여기서 이 변수명 dy는 direction y 라고 하고요 ny는 next y 라는 변수명의 약자에요. 이렇게 탐색할 수 있습니다.
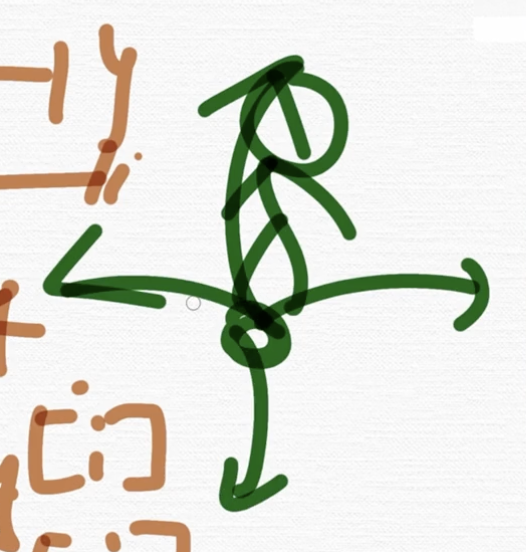
우리가 구현해야 되는 로직은 뭐였냐면 어떤 정점, 좌표계에서 4 방향을 탐색하는 로직이 필요했어요. 그래서 yx가 증가되는 것, + 1이 되건, - 1이 되건, 0이 되건 이런 것들을 우리가 알아봤죠.

그래서 그걸 기반으로 해서 dy[], dx[]라는 배열을 이렇게 정의를 했어요.
이 배열을 정의를 한 것까지는 좋아요. 그럼 이걸 기반으로 써먹어야 겠죠. 그래서 어떻게 하면 써먹을까 생각을 한 거예요.
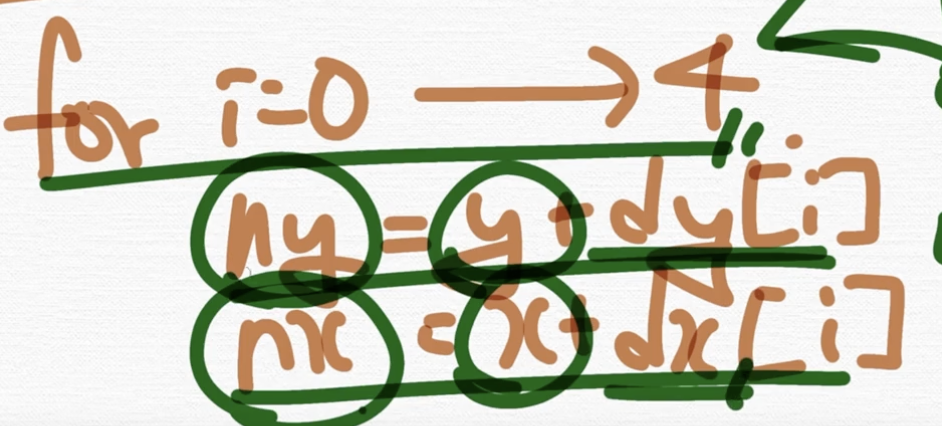
어차피 4 방향을 탐색하니까 for문이 있겠죠. 그리고 생각해보니까 우리가 방문해야 되는 정점을 정의해야하니까 지금의 좌표로부터 증감폭만 더해서 나아가야 할 정점들을 ny, nx로 정의한 겁니다.
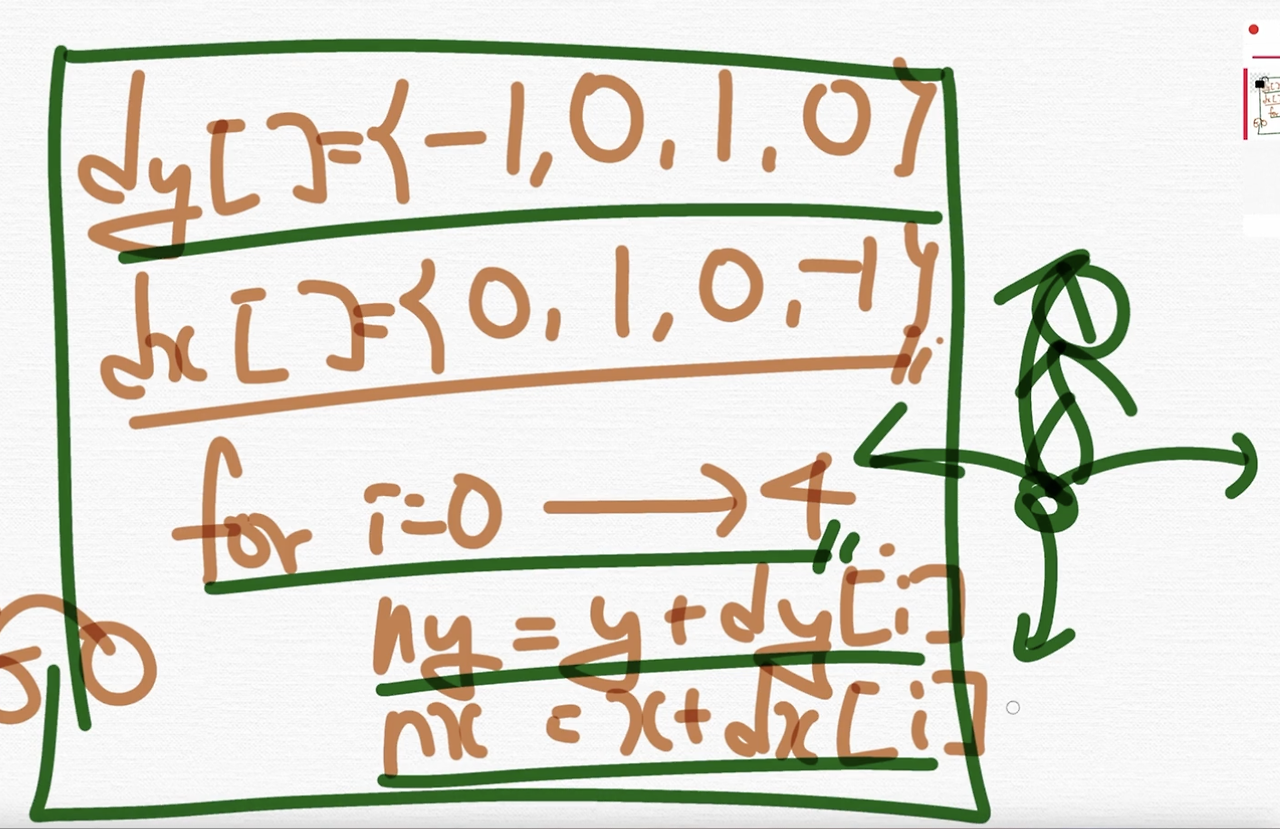
이렇게 해서 4 방향을 탐색한다고 했을 때 이렇게 생각하는 것이 하나의 세트다 라는 것을 지금까지 이해를 해봤습니다.

코드로 표현하면 이렇고, 자 이제 실습을 하면서 해보도록 할게요.

처음부터 코드를 짜본다고 가정할게요.
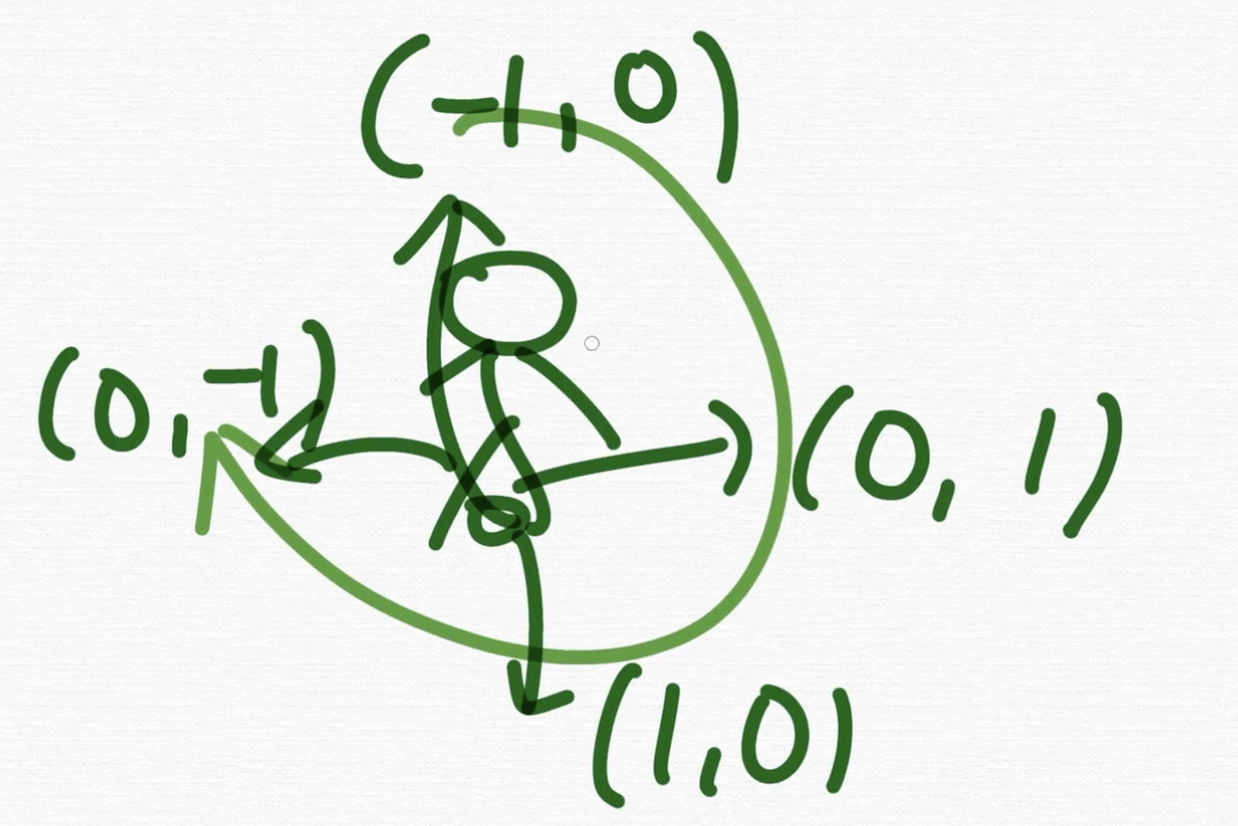
먼저 그림을 그리고나서,

코드를 짜는 겁니다. 나중되면 외우셔야 돼요.

그리고 이렇게 크기를 명시해줘도 됩니다. 똑같은 의미예요.

자, 여기서 4방향을 탐색한다. 뭔가 4번 반복해야 될 것 같애. for문 하고, 그리고 내가 움직이는 정점을 표현해야하니까 ny, nx를 정의를 해야될 것 같애. 그 다음 내가 있는 정점을 출력해볼까? 해서 출력.
이렇게 물 흐르듯이 나와야합니다.
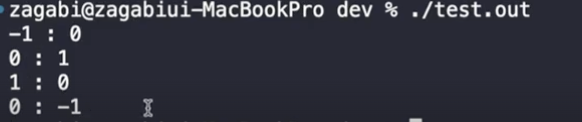
잘 출력되는 걸 볼 수 있습니다.

근데 여기서 만약에 질문, 지금까지는 우리가 4방향으로 했잖아요. 근데 사실은 문제에서 4방향이 아니라 8방향이 이렇게 주어질 때도 있어요.
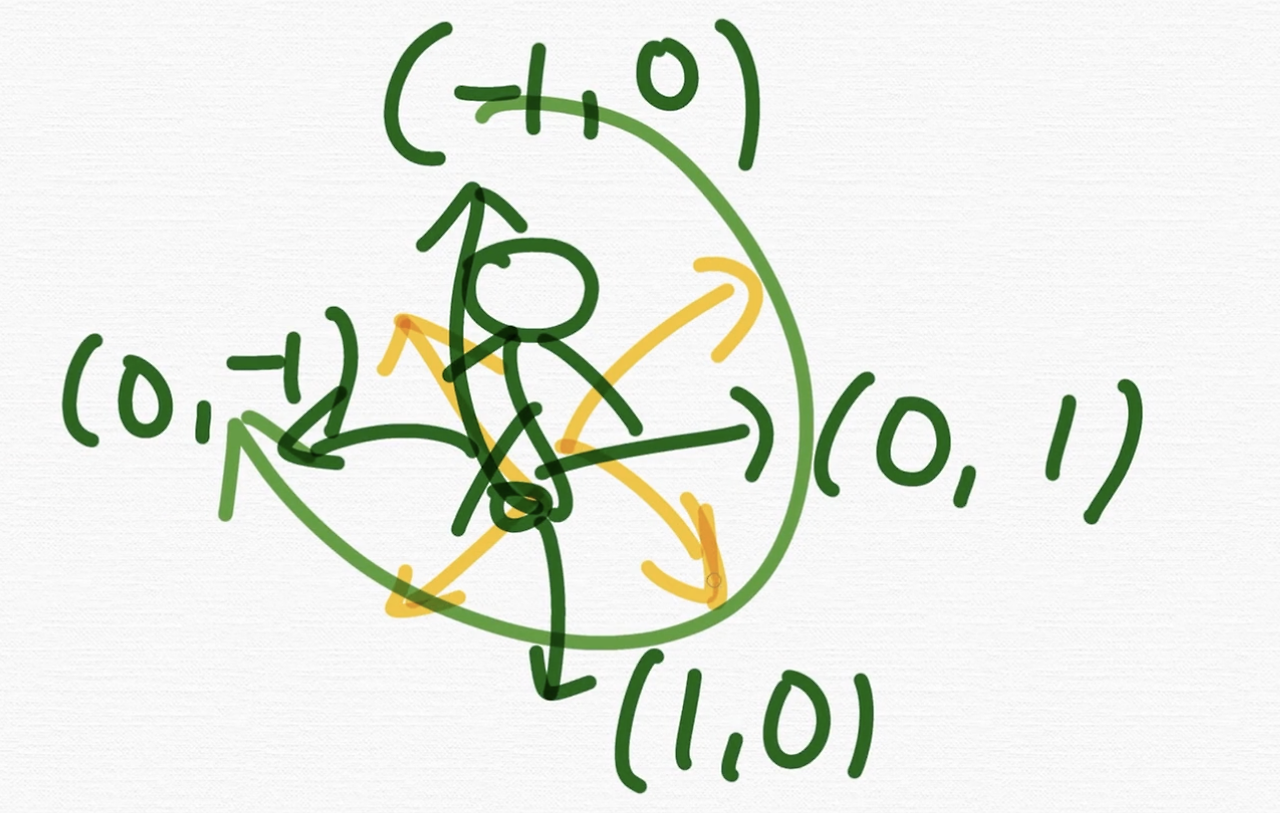
그러니까 지금 보면 이렇게 4방향으로 했지만 문제에서 갑자기 8방향이 이렇게 주어질 때도 있단 말이에요. 그러면 어떻게 해야 돼요?
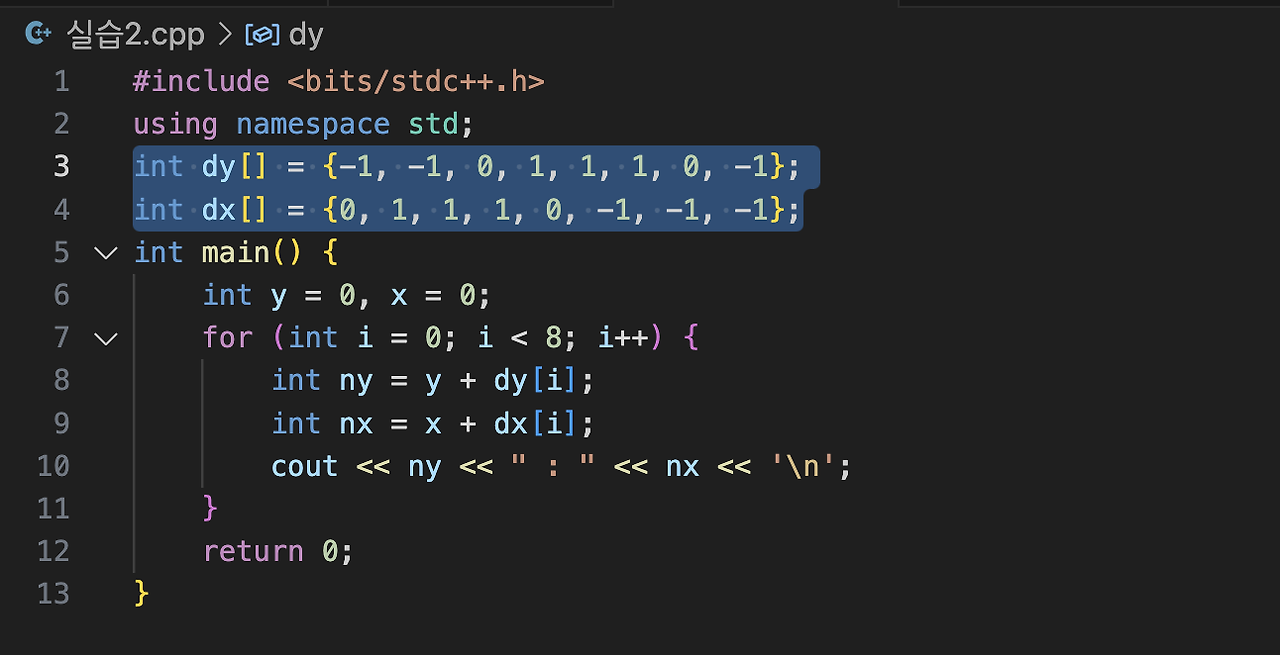
그럼 이 dy, dx 배열은 8개가 되면 되는 거예요. 그리고 이 for문은 8번 반복하면 되는 거고요.

그래서 이런 식의 코드가 완성이 되는 거죠.
이 부분을 그림으로 나타내볼게요.
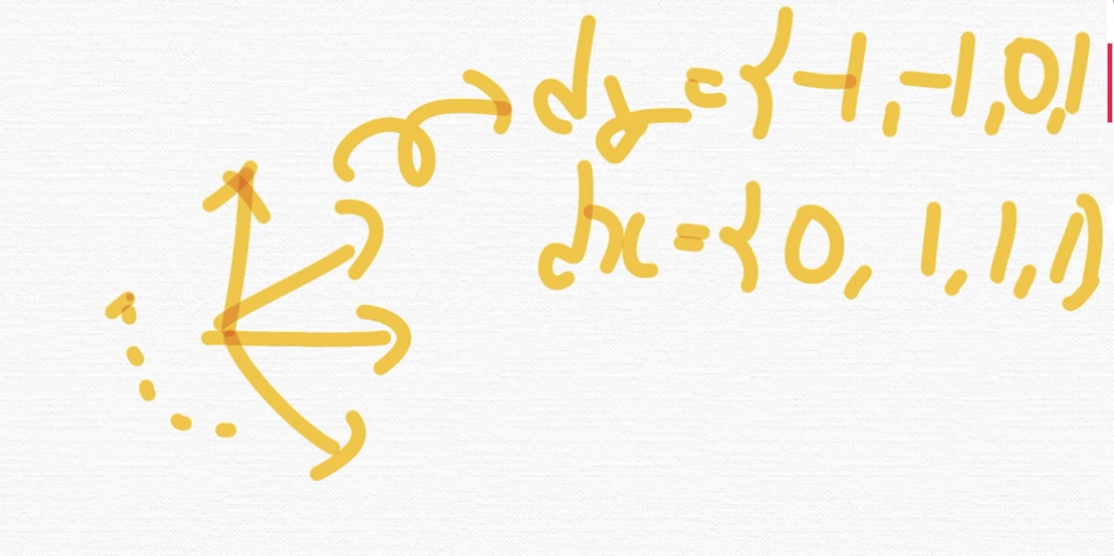
이 4개의 방향을 정의하면 저렇게 나오고, 이걸 그대로 -1 곱해서 나오면

이렇게 나옵니다.

이걸 토대로 6방향 등 문제에 따라서 코드를 구축하면 됩니다.

그러면 이번에는 문제를 한번 내보도록 할텐데, 3 곱하기 3 맵을 받아야 돼요.

이런 식으로 맵이 주어진다고 해볼게요. '

주인공은 여기서부터 시작을 한대요. 그리고 주인공은 4방향으로 탐색이 가능하고요. 그리고 정점을 방문하면서 해당 정점을 출력하는 예제 입니다. 그리고 방문한 정점은 다시 방문하지 않는 코드를 작성을 하시면 되는 겁니다.

여러분 일단은 방문한 정점은 다시 방문하지 않는다? visited 가 생각이 나야돼요.
그리고 4방향이니까 아까 설명했던 dy, dx, for문 하면서 ny, nx가 생각이 나야되고요. 어떻게 해야 될까요?

일단 3 곱하기 3짜리 맵을 입력받아서 {0, 0}부터 시작을 하는 코드예요.

정답 코드는 이렇습니다.

자 일단은 지금 n을 3으로 정의했죠. 그리고 3 곱하기 3짜리 맵을 받아야 되니까 해당 2차원 배열을 선언한거에요.
그리고 우리 방문한 정점을 방문하면 안되기 때문에 이런식으로 visited도 똑같이 한거를 볼 수가 있고, 4방향으로 탐색하기 때문에 이런 식으로 dy[], dx[]를 정의한걸 볼 수가 있어요.

자 a라는 2차원 배열을 선언을 하고 입력을 받습니다. go 라는 함수를 (0, 0)부터 시작합니다.
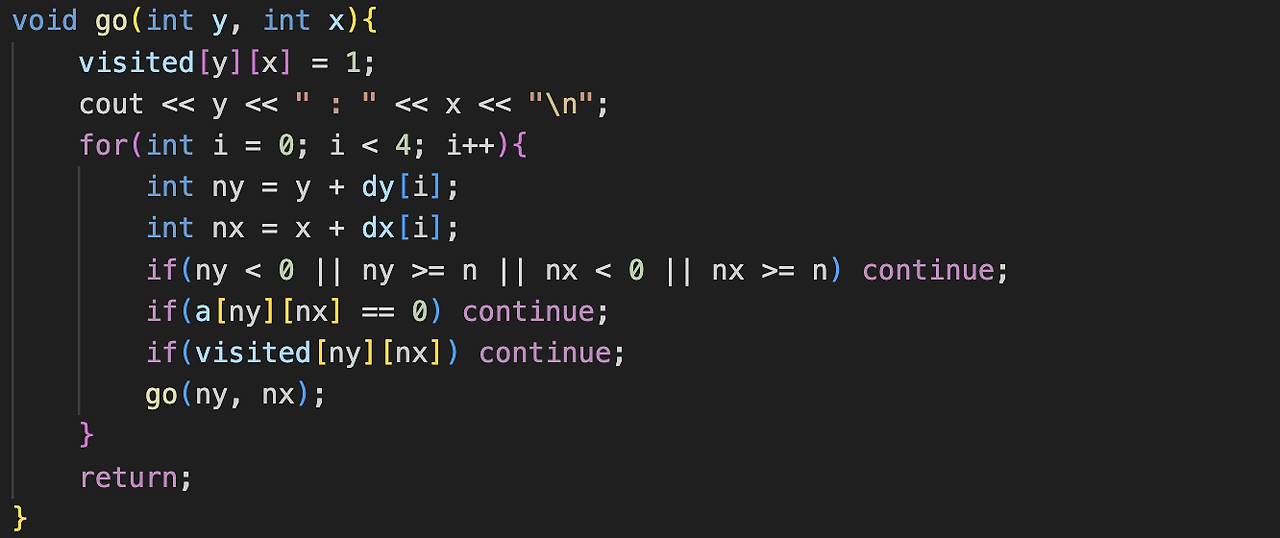
이 go 함수를 보시면 방문한 정점을 색칠하고 출력을 합니다.

이 세 가지 줄의 continue에 대해서 해보자면, 먼저 a[ny][nx]이 0이면 갈 수 없죠. 그리고 방문한 정점이라면 또 continue죠.

그리고 여러분 이게 굉장히 중요해요. 왜 그러냐면 이건 오버플로우나 언더플로우를 방지하는 코드예요.
제가 만약 2차원짜리 배열을 정의했어요.
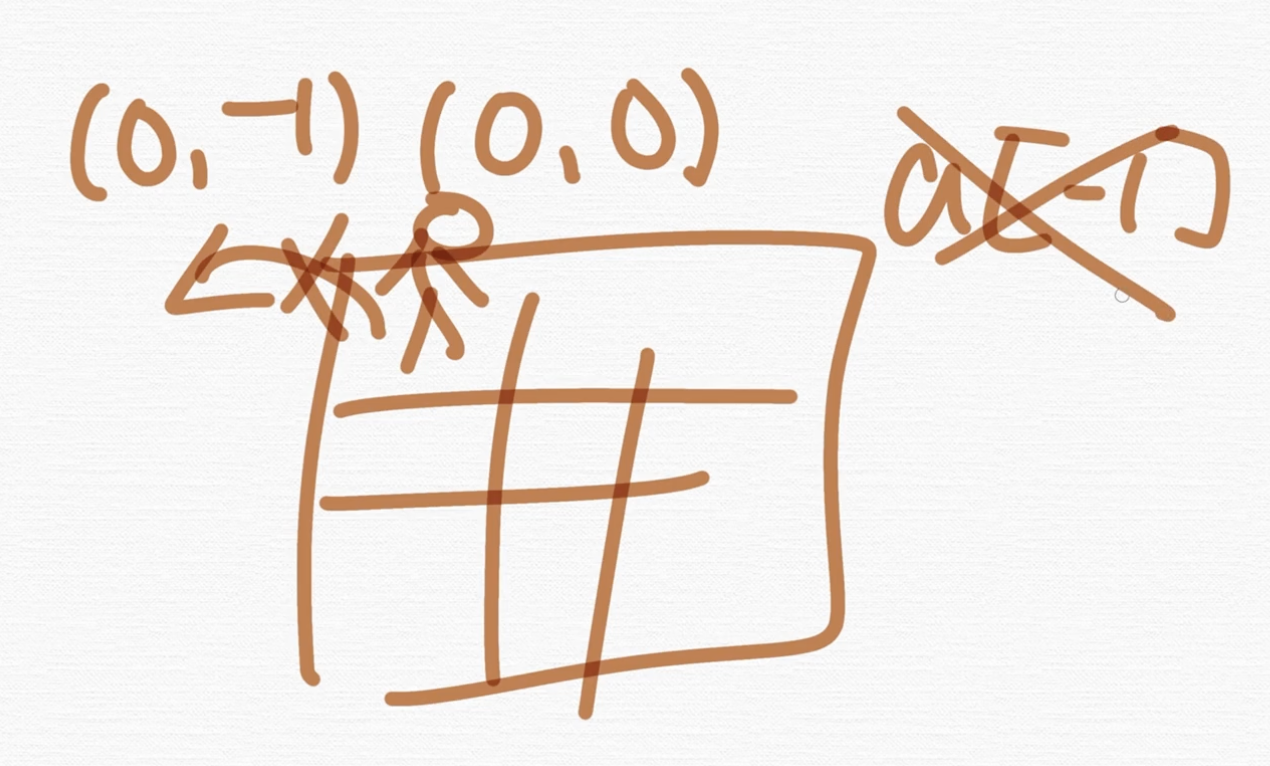
제 위치가 (0, 0)이에요. 그런데 근데 (0, -1)으로 갈 수 있다, 없다? 없습니다. 우리 배열은 마이너스를 참조 못합니다. 그래서 ny < 0 이나 nx < 0이 들어가는 거예요.

그리고 이게 3 X 3짜리 배열이니까 여기서 만약에 오른쪽으로 가게되면, (2, 3)이 되겠죠. 근데 배열이 3개짜리라면 2까지만 참조가 가능하죠. 그러니까 (2, 3)이 돼버리면 배열의 범위를 넘어서잖아요. 그래서 우리가 선언한 배열의 범위를 넘어서는지 체크하는 코드가 ny >= n, nx >= n 입니다.
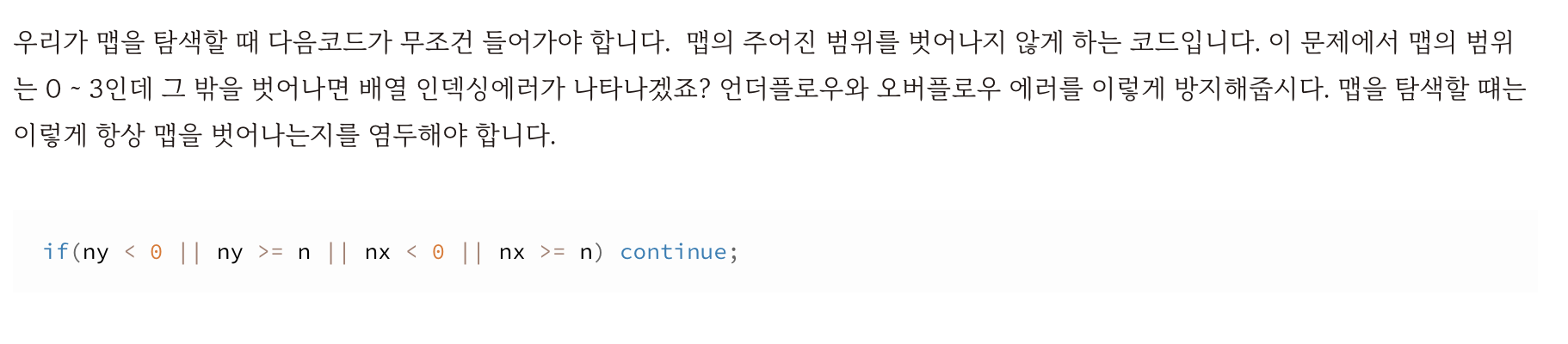
즉, 언더플로우, 오버플로우를 체크를 해서 continue 하는 거에요.

여러분들이 종종 실수하시는 부분이 있는데, 이거 순서 바꾸면 가능할까요? 불가능하죠 이미 언더플로우, 오버플로우가 발생할 수 있는데 여기서 일단 참조를 해버리잖아요.

그래서 항상 ny, nx를 정의할 때 먼저 언더플로우와 오버플로우를 체크를 하는 거에요.
이렇게 해서 인접행렬과 인접리스트가 아니라, 그냥 맵으로 주어지고 4방향 탐색을 할 때 어떻게 되는지를 알아봤습니다.
'10주완성 C++ 코딩테스트 | 알고리즘 코딩테스트 > 2주차 : 그래프이론 DFS BFS' 카테고리의 다른 글
| 2주차 개념 #9. 깊이우선탐색(DFS, Depth First Search) (0) | 2024.03.24 |
|---|---|
| 2주차 개념 #8. 연결된 컴포넌트(connected component) (0) | 2024.03.24 |
| 2주차 개념 #6. 인접행렬과 인접리스트의 차이 (0) | 2024.03.21 |
| 2주차 개념 #5. 인접리스트(adjacency list) (0) | 2024.03.20 |
| 2주차 개념 #4-2. 인접행렬(adjacency matrix) (0) | 2024.03.19 |




