당니의 개발자 스토리
2주차 개념 #8. 연결된 컴포넌트(connected component) 본문
2주차 개념 #8. 연결된 컴포넌트(connected component)
clainy 2024. 3. 24. 18:212주차 개념 #8. 연결된 컴포넌트(connected component)
오늘은 연결된 컴포넌트, connected component 라는 것에 대해서 얘기를 해보도록 할게요.
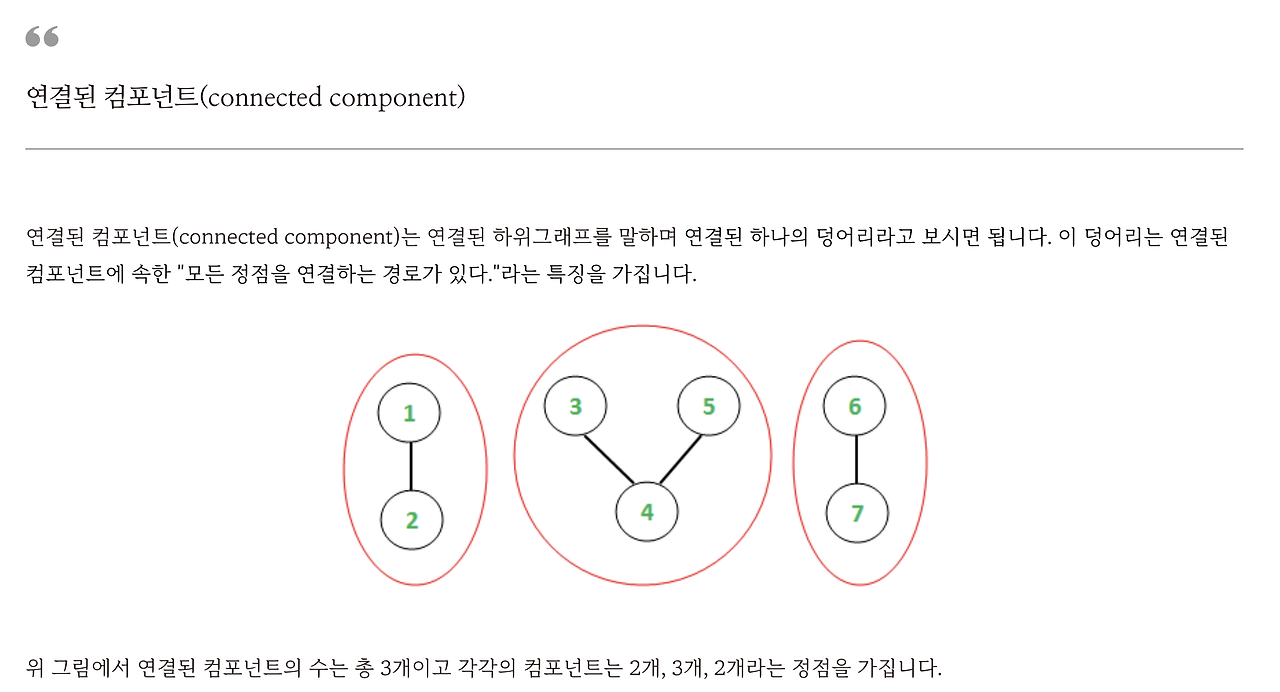
연결된 컴포넌트는 연결된 하위 그래프를 얘기를 하고요. 연결된 하나의 덩어리다 라고 보시면 돼요.
1번, 2번, 3번, 4번, 5번, 6번, 7번 이런 정점과 간선의 집합을 그래프 라고 했죠. 그래프 밑에 하위 그래프가 있는 거예요.
그러니까 지금 보시는 것처럼 1번과 2번이 서로 연결되어 있고 3, 4, 5번이 서로 연결되어 있고 6번, 7번은 서로 연결되어 있죠. 뭔가 이렇게 덩어리 세개로 나눠질 것 같다 라고 보시면 되죠.
연결된 컴포넌트가 뭐냐면 이렇게 연결된 하나의 덩어리이고요. 이 덩어리는 연결된 컴포넌트에 속한 "모든 정점을 연결하는 경로가 있다."는 특징을 가집니다.
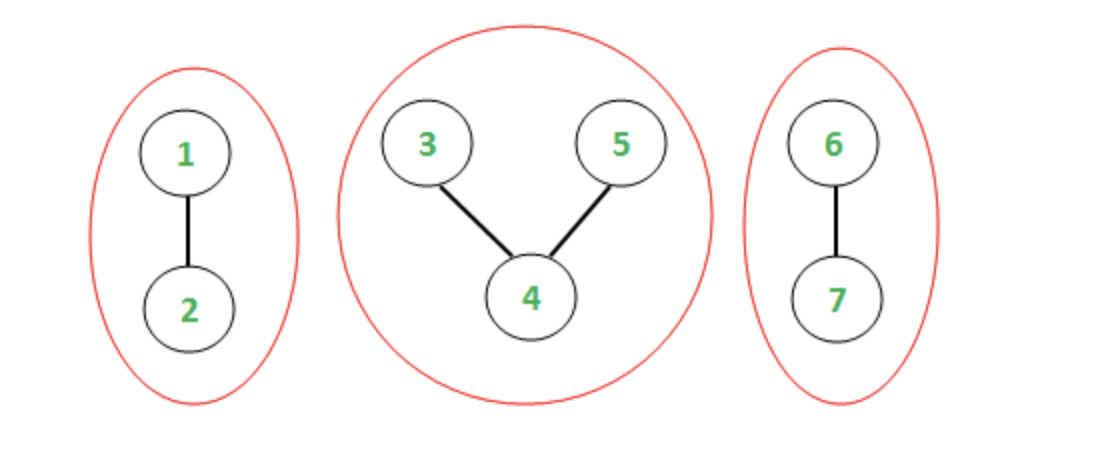
예를 들어서 3번과 5번은 직접적으로 연결되어 있지는 않죠. 그런데 지금 보시면 3번 정점과 5번 정점을 연결하는 경로가 있는 거죠. 이러한 특징을 가지는 게 바로 연결된 컴포넌트다. 서로 연결된 것끼리 이렇게 덩어리로 분리할 수 있다는 거고, 지금 위 그림을 좀 분석을 하면 연결된 컴포넌트는 총 3개예요. 3개의 덩어리가 있잖아요.
그리고 각각의 컴포넌트는 2개, 3개, 2개라는 정점을 가지죠. 조금 더 복잡한 예제를 들어볼게요.
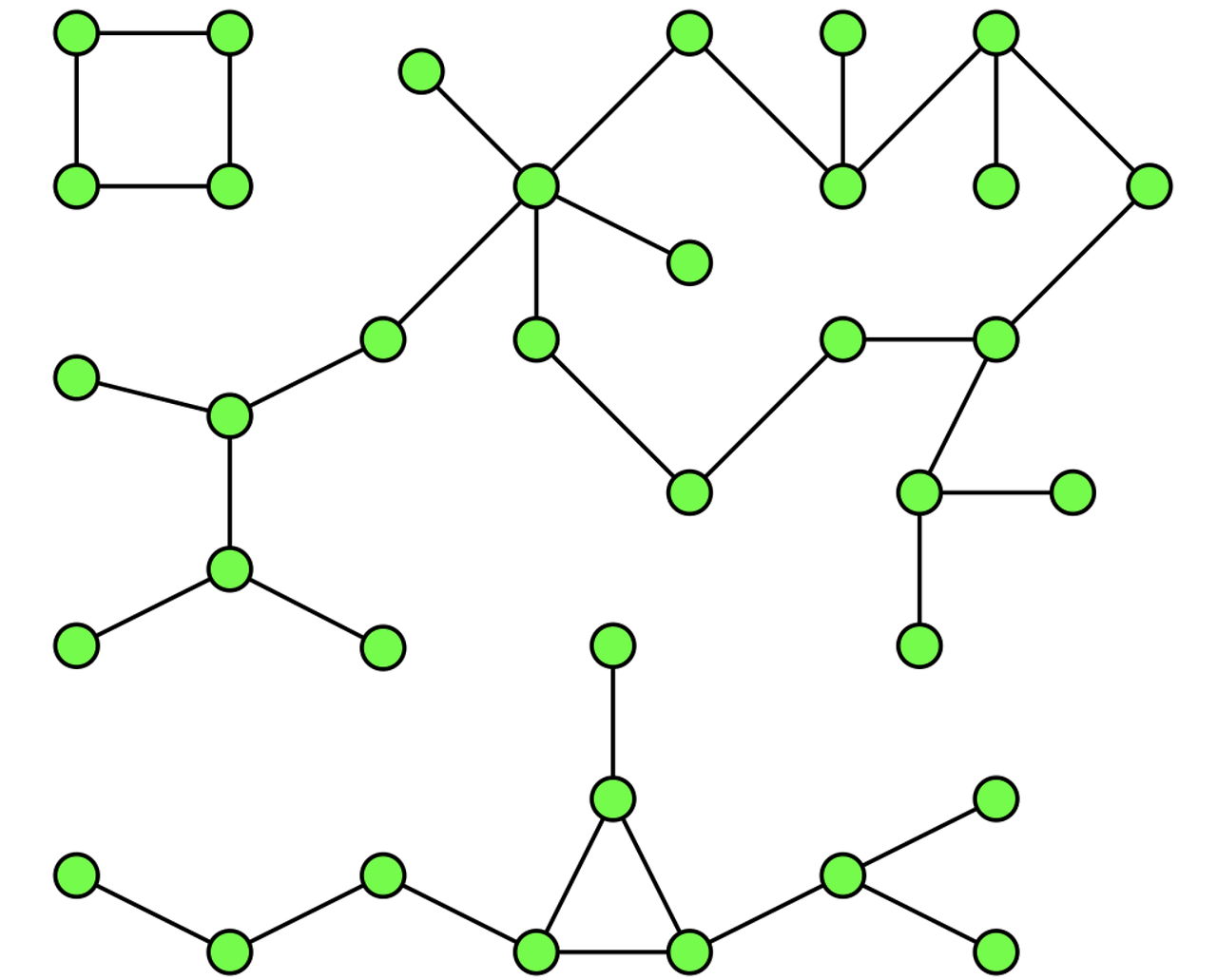

이거는 몇 개일까요? 총 3덩어리의 연결된 컴포넌트가 있는 겁니다.
제가 그림을 그리면서 설명을 해보도록 할게요.

총 몇 개의 연결된 컴포넌트로 나눌 수가 있죠? 세 덩어리죠.

하나의 덩어리가 되는 겁니다.

그리고 덩어리 안에서의 이 정점에서 이 정점은 서로 연결되진 않지만 이 컴포넌트 안에는 서로 연결되는 경로가 하나 존재하는 거죠.
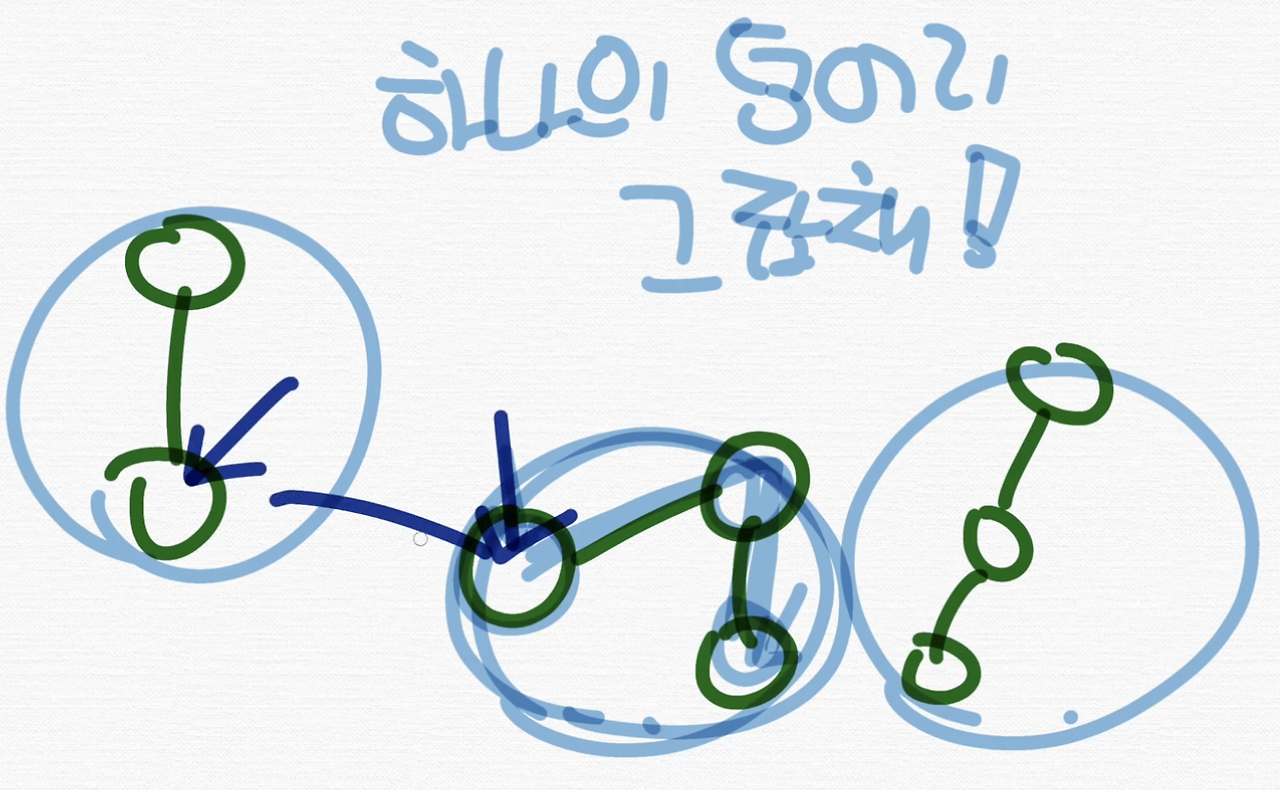
반면 이 정점과 이 정점은 서로 연결되지도 않고 가는 경로도 없잖아요. 그런 식으로 생각해서 덩어리로 나누면 됩니다.
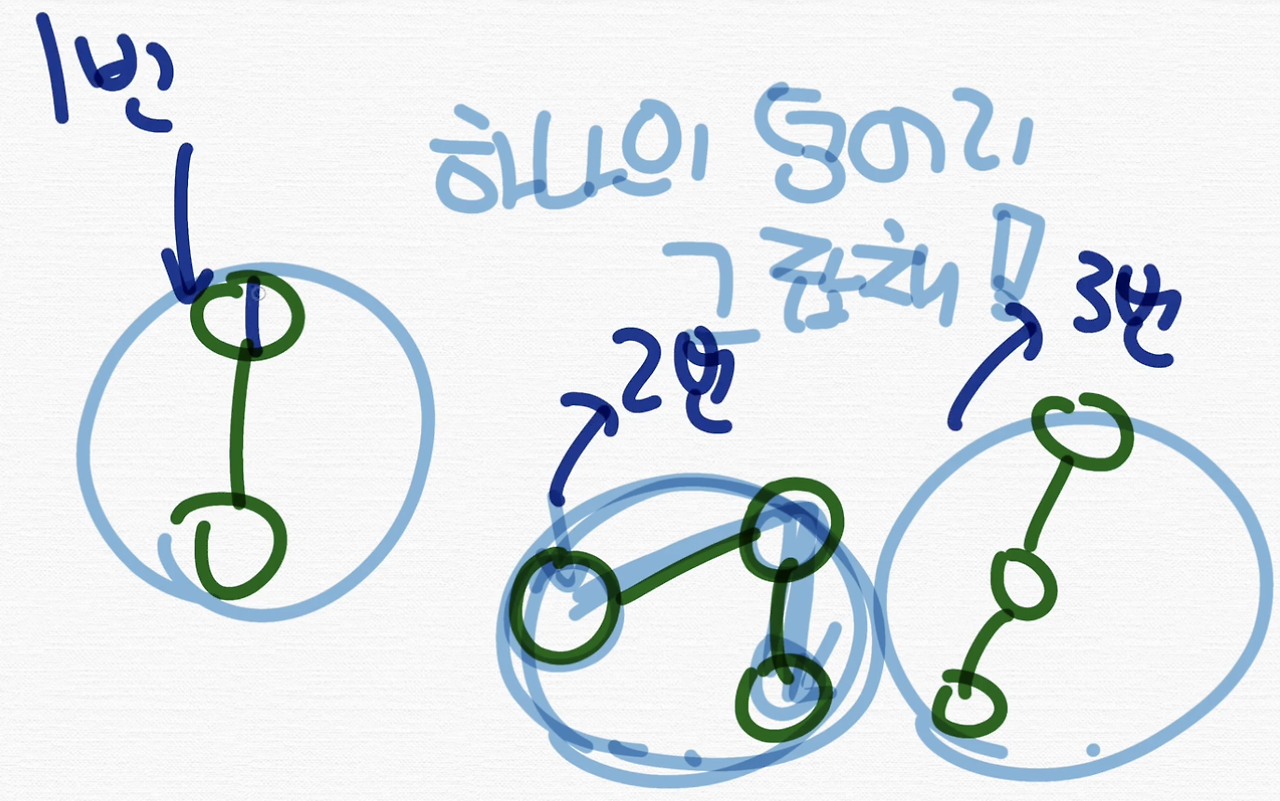
그리고 덩어리 별로 이렇게 얘는 1번으로 놓고 얘를 2번으로 놓고, 얘를 3번으로 놓아서
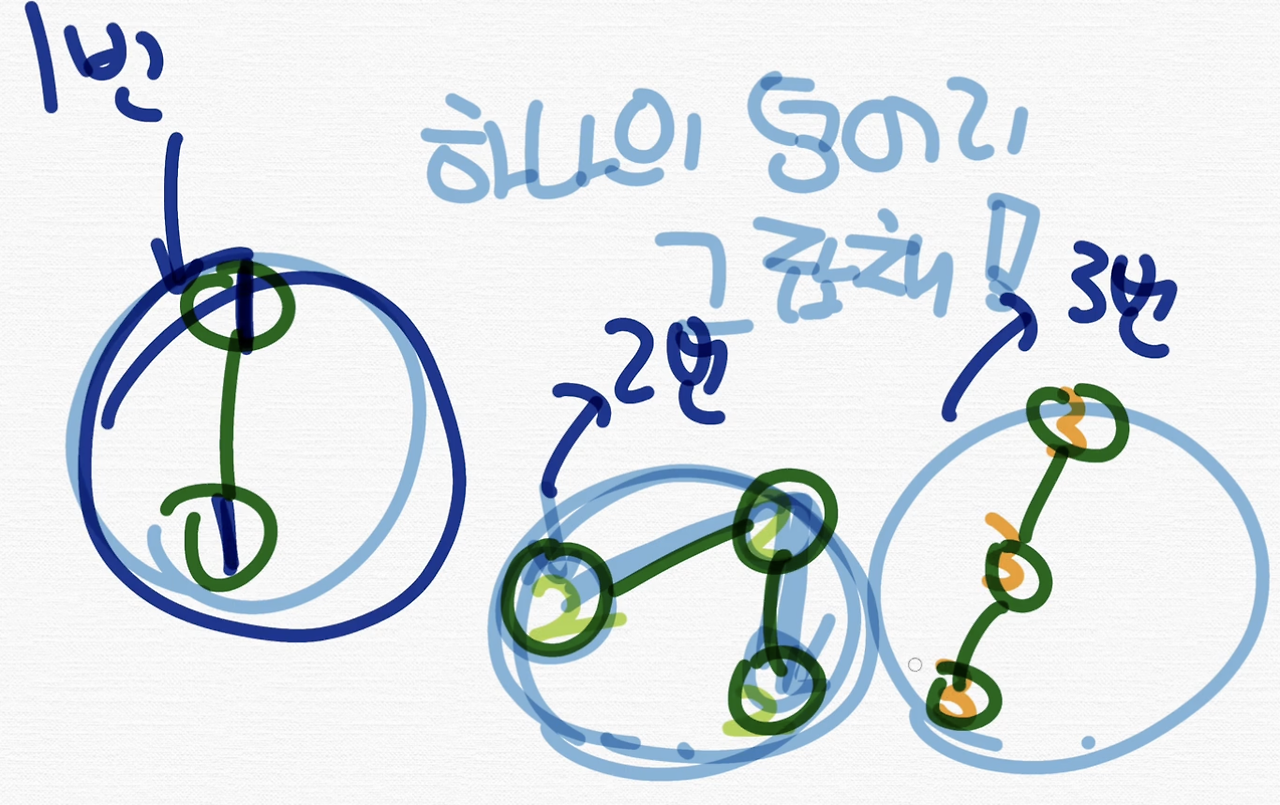
이 컴포넌트에 들어가 있는 거를 모두 1번. 이렇게 1, 1 이렇게 색칠하는 거예요. 얘는 2번으로 색칠하고 얘는 3번으로 색칠해서 이렇게 서로 id를 부여하는 것을 flood fill 이라는 알고리즘 라고 합니다.
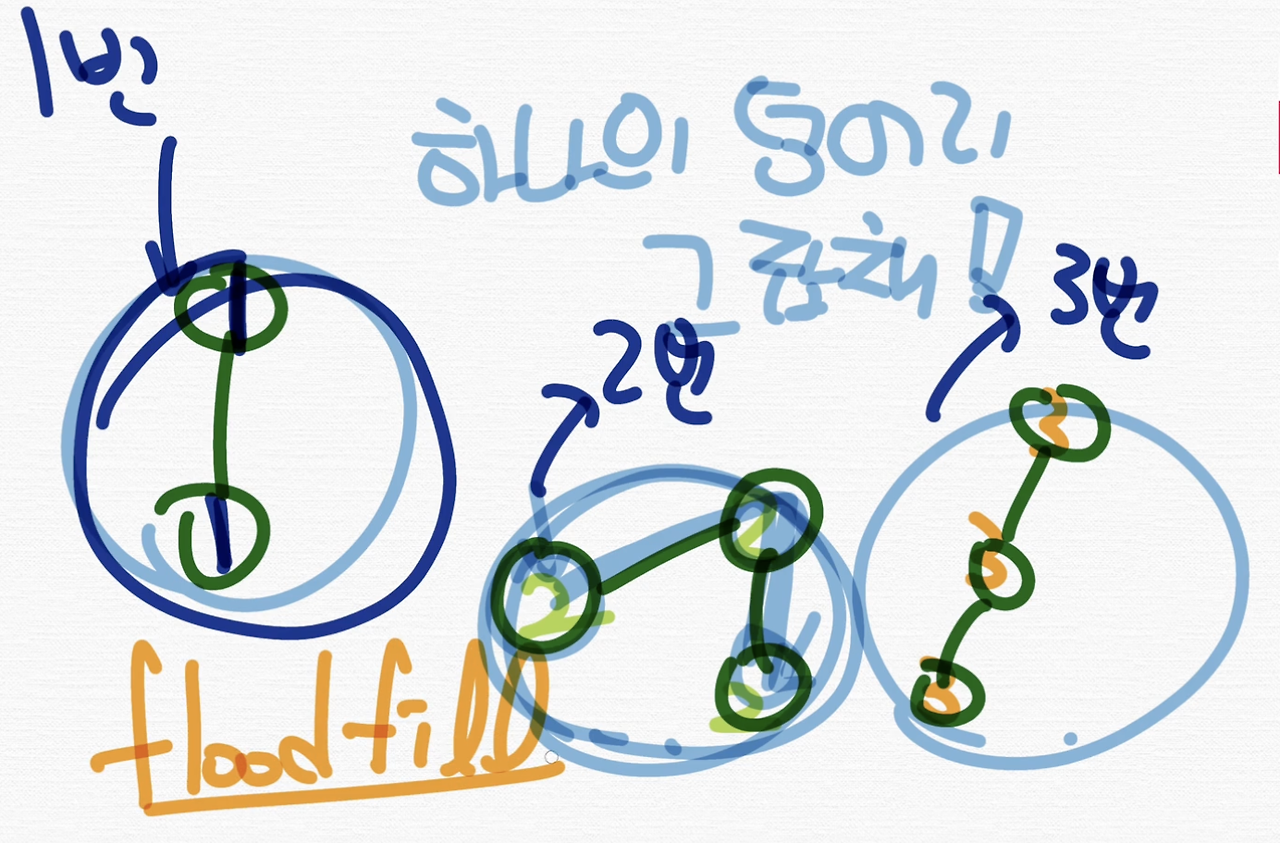
이런 Connected Components끼리 어떤 번호, 얘는 1번, 얘는 2번, 얘는 3번, 이런 식으로 번호를 부여하는 알고리즘을 flood fill 이다. 라고 보시면 되고요.
하나만 더 설명을 하고 마치도록 할게요.
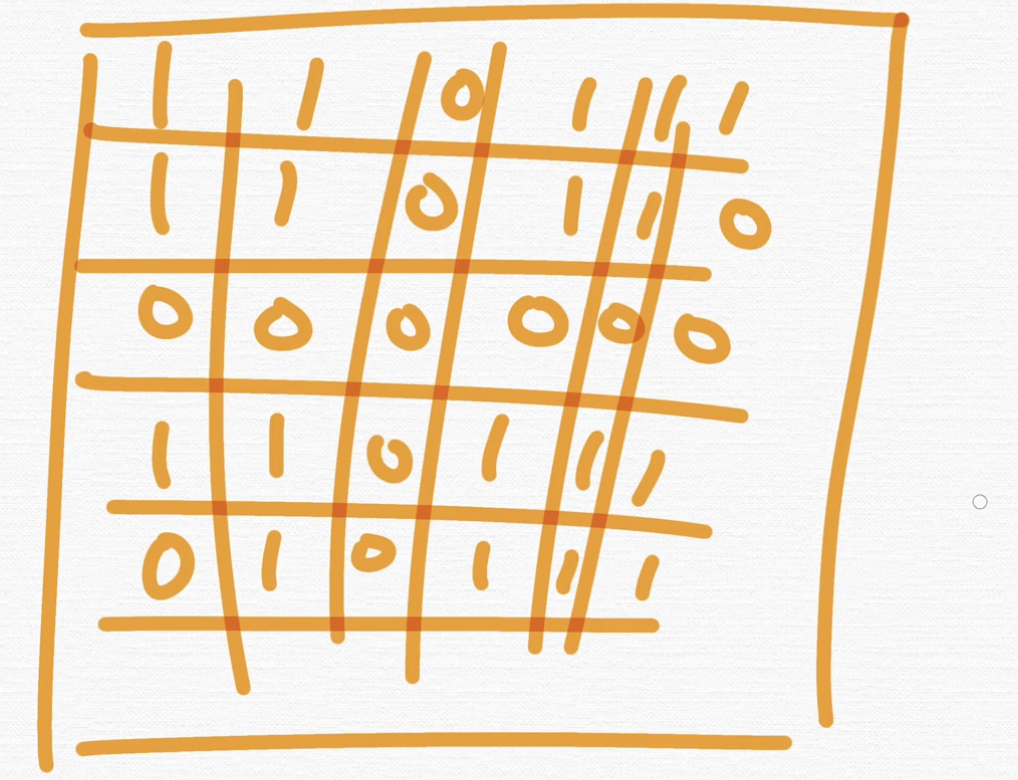
뭐냐면 저희가 앞서서 맵을 배웠죠. 어떤 맵을 우리가 정의를 해요. 1번은 갈 수 있는 노드, 즉 갈 수 있는 영역이고요. 0번은 갈 수 없는 영역이라고 할게요.

이거는 총 몇 개의 conneceted component는 라고 할까요? 1은 갈 수 있음. 0은 갈 수 없음이에요.
자, 그러면 어떻게 될까요?
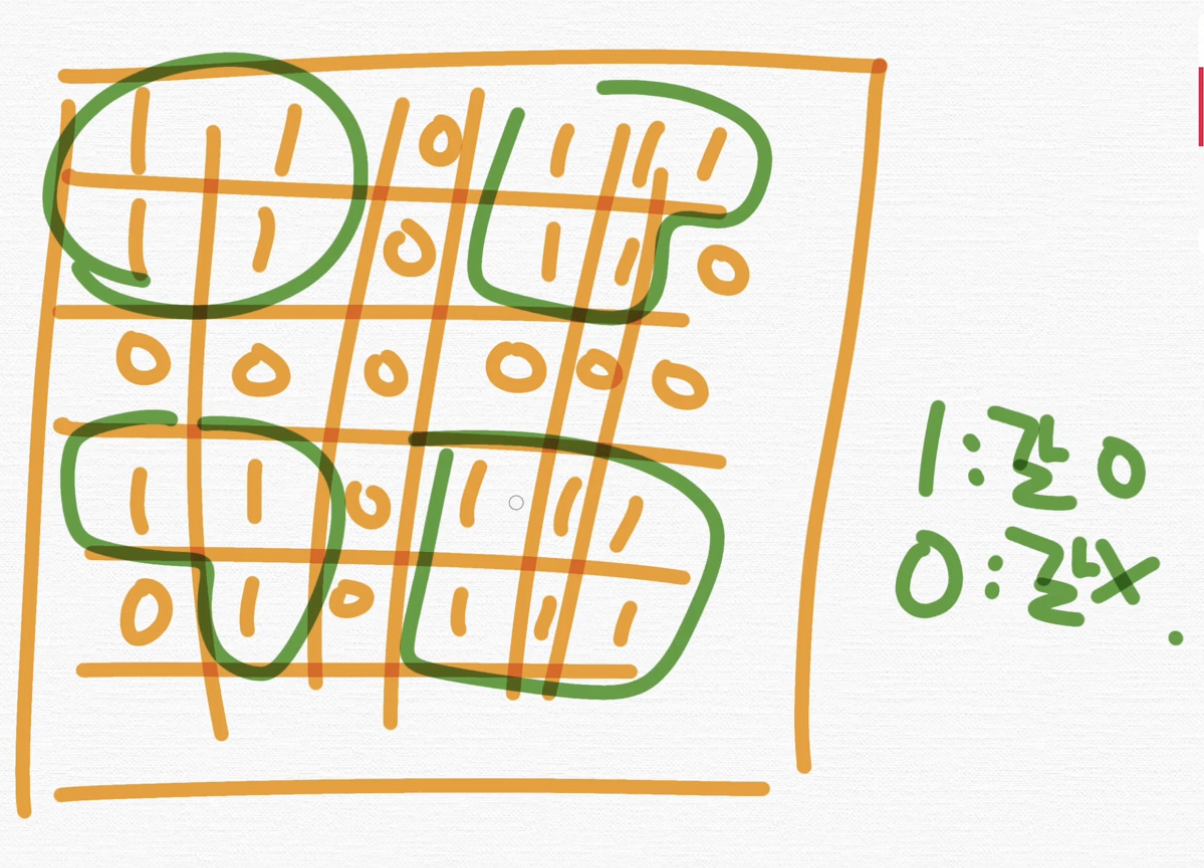
이렇게 한 덩어리씩 해서 총 네 덩어리가 있는 거죠.

이거는 이런 식으로 연결되는 정점으로 봐야된다고 했죠.

그렇기 때문에 맵으로 이렇게 주어진다고 하면, 그러니까 연결리스트 말고도 맵으로 주어질 수가 있어요.
이런 경우에도 갈 수 있는 지점들을 모아서 정점의 집합을 만들고 이걸 기반으로 Connected Component를 만든다는 거예요.
자, 다시 Connected Component 정의를 외쳐볼게요. Connected Component는 연결된 하위 그래프를 말하구요. 연결된 하나의 덩어리에요.
그리고 이 덩어리는 연결된 컴포넌트에 속한 모든 정점을 연결하는 경로가 있다라는 특징을 가진다고요.
'10주완성 C++ 코딩테스트 | 알고리즘 코딩테스트 > 2주차 : 그래프이론 DFS BFS' 카테고리의 다른 글
| 2주차 개념 #9. 깊이우선탐색(DFS, Depth First Search) (0) | 2024.03.24 |
|---|---|
| 2주차 개념 #7. 맵과 방향벡터(direction vector) (0) | 2024.03.24 |
| 2주차 개념 #6. 인접행렬과 인접리스트의 차이 (0) | 2024.03.21 |
| 2주차 개념 #5. 인접리스트(adjacency list) (0) | 2024.03.20 |
| 2주차 개념 #4-2. 인접행렬(adjacency matrix) (0) | 2024.03.19 |




