당니의 개발자 스토리

인과성과 인과추론 기본 개념 본문

LG Aimers/AI Essential Course

인과성과 인과추론 기본 개념

clainy 2025. 7. 24. 22:18

인과성이 무엇인지 설명하고 인과성과 상관성에 대한 차이를 설명 할 것임.

그리고 인과 추론을 하기 위한 기본적인 프레임워크에 관해서 설명 할 거임.

 

1부에서는 통계적 상관 관계 와 인간성이 무엇이 다른지 알아 볼 거다.

2부에서는 인과 추론의 2가지 주요 프레임워크를 소개하고 인과 효과 식별과 추정에 대해서 다룰 예정

3부에서는 다양한 인과 추론 방법들을 소개, 각각의 특징에 관해서 얘기할 거다.

 

인과 추론을 하기 위해서는 왜 이론적 틀인 프레임워크가 필요하고 가정이 필요한지에 대해 알아보자.

이것성은 어떤 한 사건이나 상태 혹은 객체가 다른 어떠한 결과를 일으키는 데 영향을 주는 것을 말한다.

이때 즉 원인이 결과에 어떻게 기여 하는지를 말하는 거다. 

 

이에 반해서 어떤 거는 다른 것과 연관 관계가 있다, 상관이 있다 라고 하는 거는 상관성만을 이야기 하는 거다.

 

토큰 인과성 vs 타입 인과성

토큰 인과성은 특별한 사건에서 나타나는 인과 관계를 다루고 타입 인과성은 일반적인 법칙을 얘기함

그래서 데이터에서 변수 간의 인과관계를 분석하는 데는 타입 인과성을 연구하는 걸로 이해하면 됨

 

기계학습(머신러닝)은 전통적으로는 데이터에 있는 상관성을 다룬다. 조건부 확률을 배움으로써 X 와 Y 사이의 관계를 학습 함.

하지만 이런 패턴은 인과성을 가지고 있지 않고 상관성만을 학습

그러나 최근에는 기계 학습에도 인과성을 활용 하려고 하는 시도가 있음

 

인과적 표상학습이나 공정성(Fairness),

공정성과 같은 경우는 인과적으로 정의가 되고 또한 딥 러닝 같은 큰 모델에서 설명 가능성(Explainability)을 접근 할 때 인과적으로 접근하기도 함.

일반 표상 학습

  • 얼굴 이미지를 보고 감정을 분류하는 CNN
  • 그런데 조명이 밝으면 ‘웃는 얼굴’로 오인할 수도 있음

→ 이건 단순한 픽셀 패턴만 학습한 것 (인과 X)

인과적 표상 학습

  • 같은 이미지에서도 조명은 원인이 아님을 모델이 학습하고
    입 모양, 눈 주름 등 진짜 감정에 영향을 주는 인과적 특성만 선택하도록 훈련

→ 진짜 원인 정보를 잘 포착하게 함

 

2. 공정성(Fairness)과 인과성

머신러닝 모델이 특정 집단(예: 소수 인종 등)에 대해 불공정한 결과를 내는 경우가 있음

회사에서 이력서를 보고 자동으로 지원자를 평가해 점수를 주는 AI 채용 시스템이 있다고 해요.

원인을 보니...

모델은 과거 데이터를 학습했어요.

  • 그런데 과거에는 소수 인종 지원자를 실제로 낮게 평가하는 편견이 있었음
  • 그 편견이 데이터에 들어가 있었고,
    AI는 그걸 학습해서 똑같이 따라함

→ 이게 머신러닝이 불공정한 결과를 내는 경우입니다.

그럼 어떻게 해결할까? → 인과 추론이 필요해요

핵심 질문:

“이 사람이 소수 인종이라는 사실이 없었더라면, 점수는 똑같았을까?”

이걸 반사실적 사고 (counterfactual thinking)라고 해요.

한편,

인공지능은 전통적으로 어떤 목적을 성취 하기 위해 조치(Action)을 수행하는 이성적인 에이전트(Agent)를 만드는 데 있다.

즉 조치를 한다는 것은 에이전트가 주어진 환경에서 상황을 바꿔서 원하는 목표(Goal)에 다가가는 것을 말함

그래서 인과성에 대한 이해가 필수적임.

 

우리가 던지는 질문이 상관성에 관한 것인지, 인과성에 관한 것인지에 따라서 어떤 식으로 데이터를 수집 할 것인가, 어떤 분석 방법을 쓸 것인가가 결정 됨.

 

데이터를 분석 하는 사람은 이러한 질문과 데이터에 대해서 상관성에 관한 건지 인과성에 관한 건지에 대한 명확한 이해필요

 

본 강의에서는 데이터가 관찰로 만들어졌을 때 개입에 의한 효과를 얻는 방법에 대해서 주로 다룰 것임.

 

이 그림은 Simpson’s Paradox (심슨의 역설)을 보여주는 유명한 예시입니다.
수술 성공률 같은 의료 데이터를 다룰 때 자주 등장합니다.
"부분을 보면 A가 더 나은데, 전체를 보면 B가 더 나은 것처럼 보이는" 역설적인 현상을 말합니다.

 

어떤 질병(예: 신장 결석)을 치료하는 두 가지 방법 A와 B가 있고,
결석 크기에 따라 Small(작은 결석), Large(큰 결석)으로 나눴습니다.

  • 성공률: P(Success∣Treatment,Stone)P(\text{Success} \mid \text{Treatment}, \text{Stone})

✅ 표 해석

결석 크기 치료 A 성공률 치료 B 성공률

Small 93% (81/87) 87% (234/270)
Large 73% (192/263) 69% (55/80)

→ 두 경우 모두 치료 A가 더 좋아 보임.

✅ 그런데 이상한 점 (Simpson’s Paradox)

전체를 합쳐보면?

치료 전체 성공률

A 78% (273/350)
B 83% (289/350)

→ 갑자기 치료 B가 더 좋아 보임!
→ 이게 바로 Simpson's Paradox예요.

❓ 왜 이런 일이 벌어질까?

이유는 환자 분포(구성 비율)가 다르기 때문입니다.

  • 치료 A는 어려운 환자(큰 결석)를 많이 받았고
  • 치료 B는 쉬운 환자(작은 결석)를 더 많이 받음

즉, Small과 Large에 해당하는 환자 수가 달라서

A는 어려운 케이스에서 성능이 좋았지만
전체 집계에서는 쉬운 케이스가 많은 B가 더 좋아 보이게 된 겁니다.

📌 핵심 개념 요약

구분 설명

조건부 성공률 P(Success∣Treatment,Stone)P(\text{Success} \mid \text{Treatment}, \text{Stone}) A가 항상 더 높음
전체 성공률 P(Success∣Treatment)P(\text{Success} \mid \text{Treatment}) B가 더 높게 나옴
왜 이런 일이? B는 쉬운 케이스(Small stone)가 많음
결론 단순 전체 평균만 보면 오해할 수 있음 → 조건부 분석이 중요함!

🎯 인과추론 관점에서의 교훈

  • 단순히 상관관계만 보면 잘못된 결정을 할 수 있음
  • 교란변수(confounder)인 "결석 크기"를 고려하지 않으면 인과적 효과를 잘못 해석함
  • 이럴 땐 조건부 확률이나 인과그래프(DAG)를 써야 진짜 인과 효과를 알 수 있음

 

실제 상황에서는 우리가 관측 하지 못한 교란 변수가 있을 수 있기 때문에 쉽지 않다.

SES(Socio-Economic Status)는 사회 경제적 지위를 말한다.

만약에 환자의 옷 상태를 보고 경제적 수준을 고려해서 저렴한 약을 처방 했다면 어떻게 되었을까?

만약에 신장 결석 사이즈만 조정해서 인과 효과를 계산 했다면 값에 왜곡이 있었을 거다.

 

이처럼 우리가 모르는 교란 변수가 있을 수 있기 때문에 인과 추론은 신중하게 접근 해야 된다.

 

우리가 심슨의 역설을 통해서 얻을 수 있는 교훈이 있음

첫 번째 인과 분석을 하기 위해서는 도메인 지식, 즉 배경 지식이 중요하다. 어떻게 데이터가 만들어지는 지에 대한 이해가 필요

 

두 번째 데이터가 똑같아 보이더라도 그 뒤에 숨겨진 인과 구조가 다르다면 다른 식으로 인과 추론을 수행 해야 한다는 점이다.

그 말인 즉슨 인과 추론을 하는 데 있어서 순수한 통계적 규칙은 존재하지 않는다.

즉 데이터만 가지고 우리가 인과 추론을 할 수는 없다. 같은 데이터라도 인과성에 대한 질문을 한다면 상관성에 대한 질문을 하는 것과는 다른 방법이 사용 되어야 할 거다.

 

우리가 궁극적으로 필요한 것은 현실세계의 인과 구조를 설명할 수 있는 수학적 모델

이 모델은 인과적 직관을 표현할 수 있어야 함.

 

Black Box System: 우리가 알고 싶은 인과 관계가 숨어 있는 세상 (예: 약이 효과 있는지?)

우리는 세상을 관찰하거나 실험을 해서 인과 효과를 알고 싶음

요소 뜻 예시

Observational Study 그냥 관찰만 한 연구 건강검진 데이터, 병원 진료기록
Clinical Trials **개입(intervention)**이 있는 실험 A 약 먹은 그룹 vs 안 먹은 그룹 비교 실험
Drug Efficacy 약의 효과 "이 약이 병을 낫게 했는가?"
Public Policy 정책 효과 측정 "최저임금 인상이 고용에 영향을 줬는가?"

 

인과 추론에는 대표적으로 두 가지 프레임워크가 있어요:

  1. Potential Outcome (PO) Framework
  2. Structural Causal Model (SCM)

이 둘은 서로 다르지만 수학적으로 연결됨

 

Potential Outcome Framework는 "만약에 ~~했더라면?"을 다루는 이론이에요.

반사실적 기반 프레임워크임.

예: 신약 A의 효과를 알고 싶어요.

  • 어떤 환자가 A 약을 먹고 병이 나았다고 해요.
  • 그런데 그 환자가 약을 안 먹었을 때는 어땠을까?
    → 그건 관찰할 수 없어요. 이미 약을 먹었으니까.

🌱 Potential Outcomes 용어

기호뜻
Y(1)Y(1) 그 환자가 약을 먹었을 때 결과
Y(0)Y(0) 그 환자가 약을 안 먹었을 때 결과
 

❗문제점: 둘 다는 절대 동시에 못 봐요!

  • 그래서 이론에서는 이걸 **“Missing Data Problem”**이라고 불러요.
  • 어떤 사람의 두 결과 중 하나는 항상 빠져 있음

💡 그래서 어떻게 인과 추론을 하냐면?

  • 약을 먹은 사람과 안 먹은 사람을 비슷한 조건으로 잘 맞춰서 비교
  • 예: 나이, 성별, 병력 등이 비슷한 사람끼리 짝지어 비교

📌 이 프레임워크가 어디에 쓰이나요?

  • 의료 (약물 효과 분석)
  • 공공 정책 평가 (최저임금, 교육 정책)
  • 경제 실험
  • 광고 실험 (광고 A vs 광고 B 보여주기)

Structural Causal Model (SCM)란?

이 모델은 인과를 수학적 함수와 그래프(DAG)로 표현합니다.

세상은 변수들 사이의 인과 관계로 이루어져 있고,
우리는 그 관계를 **방향 있는 그래프(DAG)**로 표현할 수 있다!

📌 아주 쉬운 예시

🎓 학교 공부 → 시험 점수 예제

  • X: 공부 시간
  • : 시험 점수

X → Y
(공부량이 시험 점수에 영향을 줌)

 

이런 구조를 SCM에서는 인과 그래프로 그리고,
이 관계를 수학 함수로 표현

                                 Y = f(X,U)

  • f: 공부량이 시험 점수에 어떻게 영향을 주는 함수
  • : 관찰되지 않은 잡음(예: 컨디션, 운 등)

SCM에서의 개입(do)

예:

  • : 그냥 관찰된 확률
  • : 진짜로 흡연하게 했을 때 결과

👉 이 둘은 다릅니다
👉 do는 개입(intervention)을 의미해요. 인과추론의 핵심 도구!

SCM은 인과 관계를 구조적으로 표현 하는 데 중점을 둔다. 그래서 각 변수들이 어떻게 결정 되는지 정의하고 있는데 이때 변수마다 어떠한 다른 변수들이 영향을 주고 있는지, 다른 노이즈들이 영향을 주고 있는지를 정의하게 된다.

이런 구조적 정의를 합치면 변수 간의 인과 관계를 알 수 있고 그래프(DAG)로 표현할 수 있다.

 

직관적으로 이해를 해보면 우리가 관찰 하게 되는 변수 V만으로는 인과 관계를 다 설명할 수 없기 때문에

이 변수에 영향을 주는 다른 변수 U에 대해서 생각해야 하는 것이고

이때 우리가 모르는 변수는 어떠한 분포를 따르지만,

우리가 관찰하게 되는 변수는 결정적인 함수(Deterministic Function)에 따라서 결정 된다고 생각하는 것이다.

 

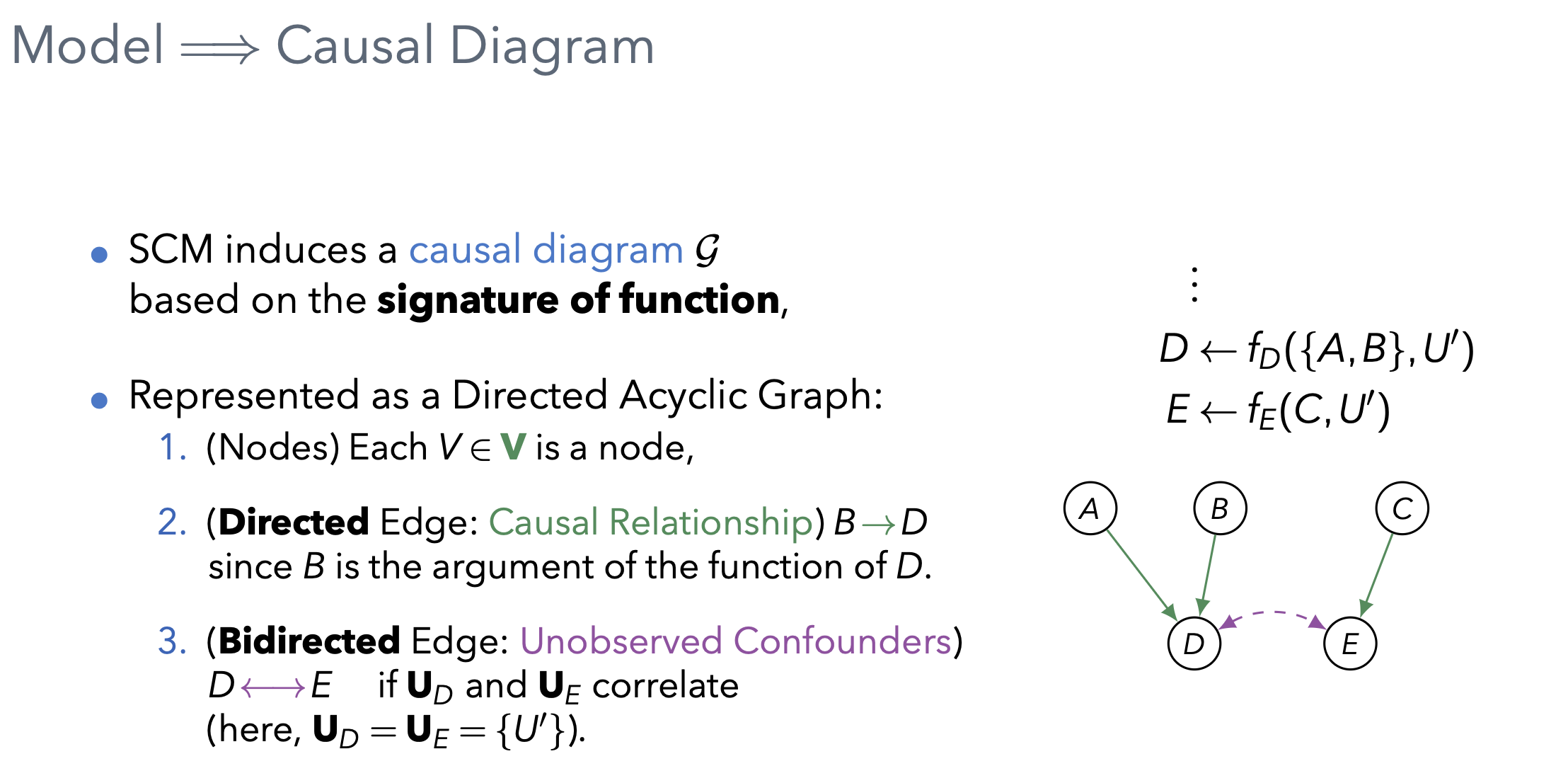
노드들은 우리가 관측하는 내생변수 V,

내생변수 간의 인과관계를 보면

A, B에 의해 영향을 받고 있는 D 가 있고, U'라고 하는 외생변수(관측X)에 영향을 받고있는 D, E 관계는 양방향 엣지로 표현함.

이 D, E 두 변수 사이에 우리가 모르는 교란 요인에 의해서 영향을 받고있다고 표현할 수 있음

 

SCM에서 개입을 한다는 건 특정 변수를 상수로 고정하는 것을 의미함.

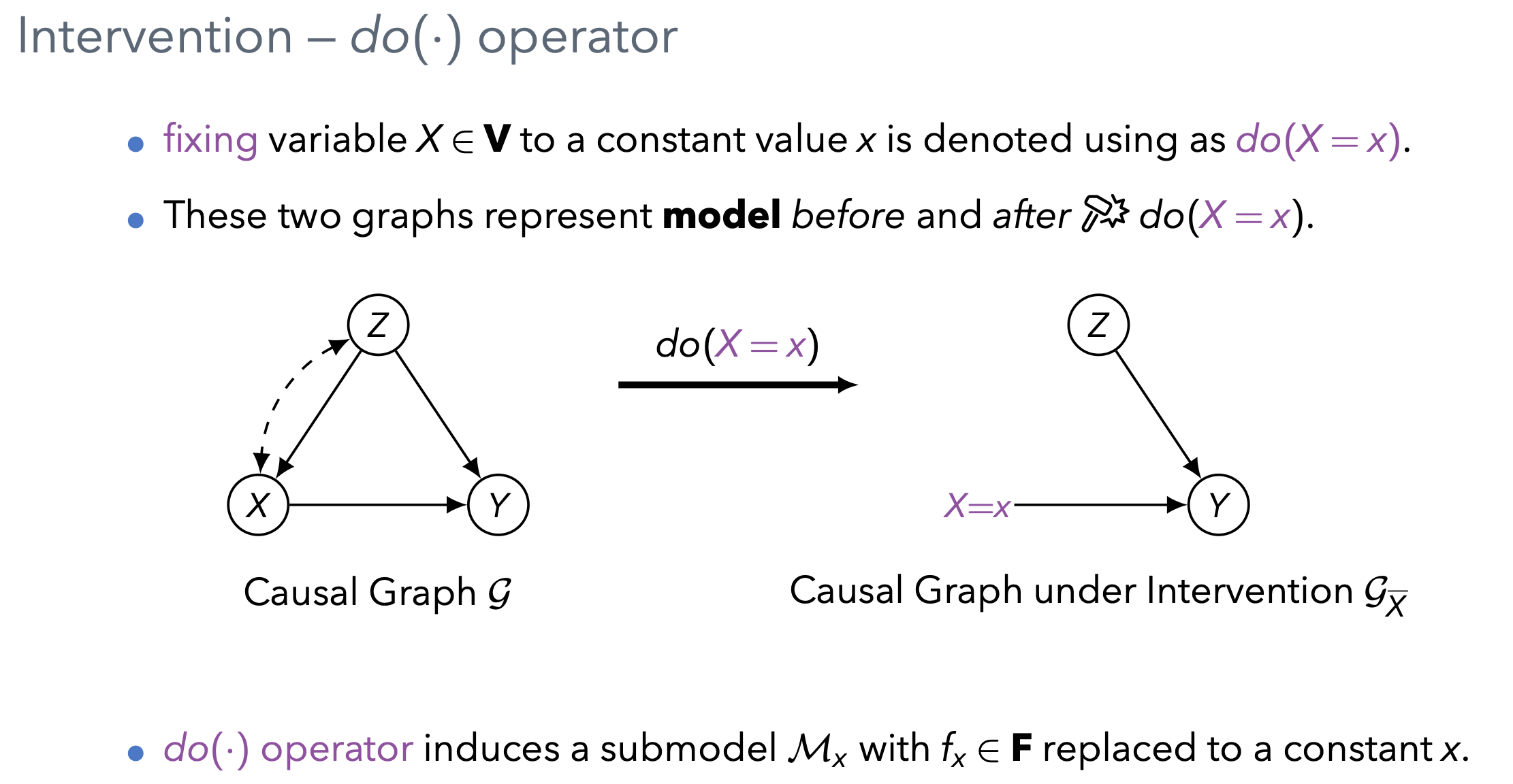
X라는 변수를 고정 하기 위해 개입을 한다면 X라는 변수는 더 이상 Z와 같은 모르는 교란 요인들들에게 영향을 받지 않고 상수 X로 고정되기 떄문에 원래 있던 오른쪽과 같은 그래프에서 엣지를 지우는 것으로 이해할 수 있음.

 

SCM은 데이터가 어떻게 만들어지는 지에 대한 가정을 함.

 

"커피를 마시면 정말로 잠을 못 잘까?"

이걸 알고 싶다고 해볼게요.

🔍 그런데 문제가 있어요

커피 마신 사람들 보면...

  • 대부분 스트레스를 많이 받아서 마셨어요
  • 스트레스가 많은 사람은 커피 때문이 아니어도 잠을 잘 못 자요

그래서 우리는 커피를 마신 사람들이 잠을 못 잔 걸 보고도 헷갈려요:

"진짜로 커피 때문에 잠을 못 잔 걸까?
아니면 스트레스 때문에 커피도 마시고, 잠도 못 잔 걸까?"

💥 이걸 구분하려면 어떻게 해야 할까요?

그냥 관찰만 해서는 안 돼요:

  • "스트레스가 많은 사람들이 커피 마셨네?" → 이건 관찰이에요

✅ 그래서 등장한 게 do(X = x) 라는 기호

이건 무슨 뜻이냐면
"우리가 직접 개입해서 커피를 마시게 해보자!"
라는 뜻이에요.

📌 핵심 차이

표현 의미

`P(잠 못 잠 커피 마심)`
`P(잠 못 잠 do(커피 마심))`

🧠 그림 다시 해석

왼쪽 그림 (개입 전)

Z (스트레스) → X (커피)
Z (스트레스) → Y (잠 못 잠)
X (커피)     → Y (잠 못 잠)

→ 커피와 잠 사이의 관계에는 **스트레스라는 혼란 요소(Z)**가 섞여 있어요.

오른쪽 그림 (do 연산 후)

Z (스트레스)    X (강제로 고정됨)
Z (스트레스) → Y (잠)
X (커피)     → Y (잠)

→ Z → X 화살표가 사라졌어요!

왜? 우리가 X를 직접 고정시켰기 때문에
더 이상 스트레스(Z)가 커피(X)를 좌우할 수 없게 된 거예요.

✅ 결론

do(X = x)는
**“X를 직접 조작해서 Y에 어떤 변화가 있는지 알아보자”**는 뜻이에요.
그래야 진짜 인과 효과를 파악할 수 있어요.

🎬 비유로 마무리

  • 관찰: “운동 많이 한 사람들이 건강하네!” → 사실은 원래 건강해서 운동 많이 한 걸 수도 있음
  • 개입(do): "운동을 직접 시켜보고 진짜 건강해졌는지 보자!"

 

'LG Aimers > AI Essential Course' 카테고리의 다른 글

인과추론을 위한 다양한 방법과 특징  (0) 2025.07.25
인과추론을 위한 두가지 프레임워크  (0) 2025.07.25
수요 예측 실습 및 사례 분석  (0) 2025.07.24
수요 예측 기법  (0) 2025.07.23
공급망 관리 기본 개념  (0) 2025.07.23
'LG Aimers/AI Essential Course' Related Articles more