당니의 개발자 스토리
2주차 개념 #5. 인접리스트(adjacency list) 본문
2주차 개념 #5. 인접리스트(adjacency list)
오늘은 인접 리스트에 대해서 배워보도록 하겠습니다.

저희가 앞서서는 인접행렬에 대해서 배웠죠. 인접행렬은 2차원 배열을 기반으로 그래프를 표현한다고 했죠.
그런데 인접 리스트는 2차원 배열이 아니라, 연결 리스트를 여러 개 만들어서 그래프를 표현하는 방법이다. 라고 보시면 됩니다.
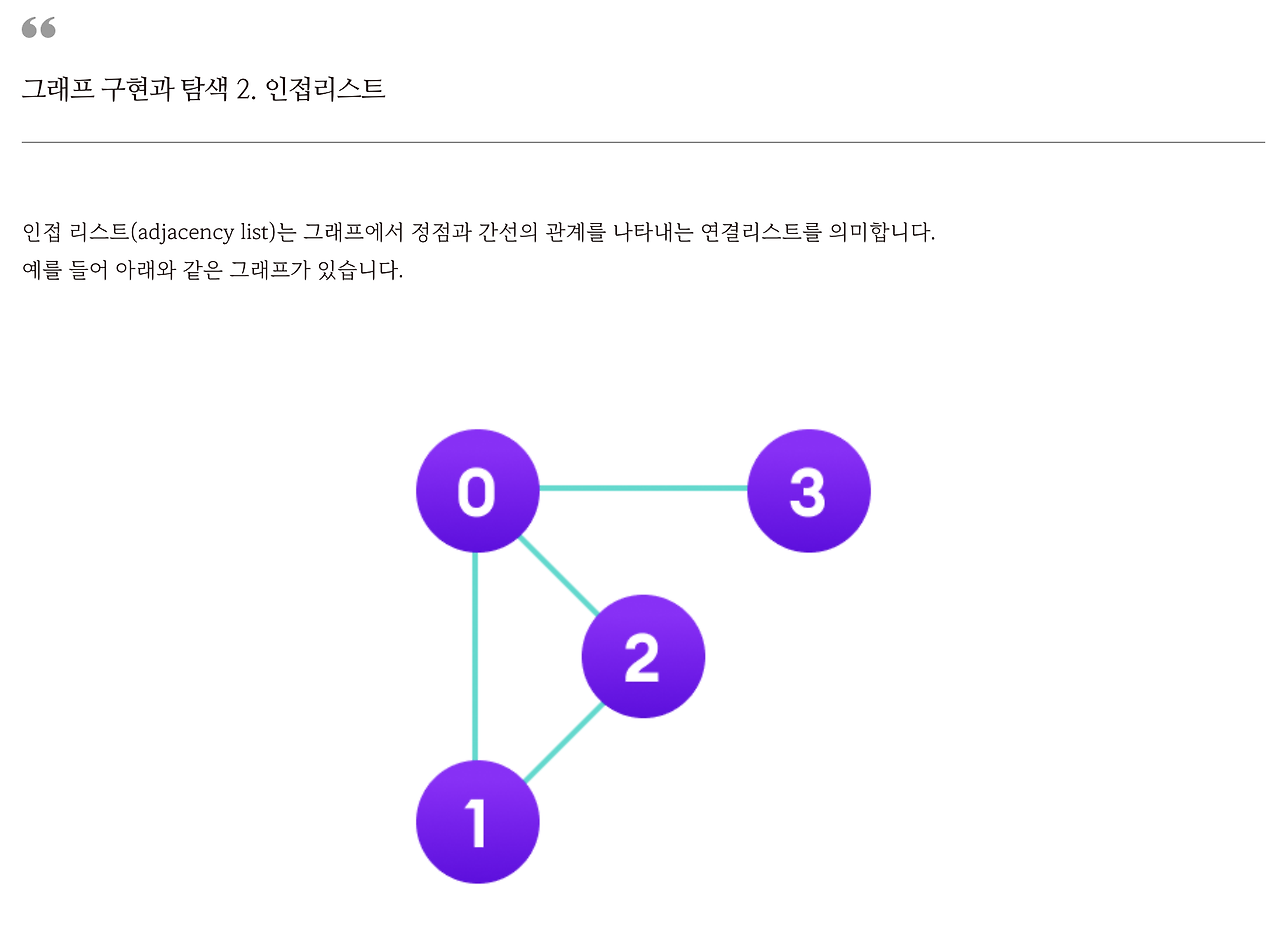
예를 들어서 이런 그래프가 있어요. 이걸 어떻게 연결 리스트로 표현할까? 정점마다 연결 리스트를 만드는 거예요.
정점이 몇 개? 4개죠.

이 4개의 정점마다 연결 리스트를 만들어요.

그리고 여기다가 연결된 정점들을 다 집어넣어요. 그러니까 각 정점마다 연결 리스트를 만들고, 그 연결 리스트에다가 연결되어 있는 정점만 집어 넣는 거예요. 연결되지 않은 정점은 신경 쓰지 않는 거예요.
우리가 앞으로 연결 리스트를 구현할 때 변수명을 adj, adjacency 라는 변수명을 쓸 거예요. 여러분들이 인접 리스트 관련해서 어떤 글을 보거나 어떤 영상을 보면 보통의 변수명이 adj 라고 되어 있는 걸 볼 수가 있어요.
인접 리스트를 영어로 adjacency list 라고 하는데 앞글자만 딴 거예요.
우리는 adjacency 라는 연결 리스트를 몇개 만들어야 되나요? 지금 정점이 4개니까 4개 만들어야 하죠.

이거 4번째의 Adjacent를 나타내는게 아니라, 4개까지 만들어야 된다는 거에요.
자 예를 들어서 0번 정점과 연결되는거는

adj[0]에다가 push_back을 하면 되겠죠.

1번에다가는 0, 2를 push_back 하면 되죠.
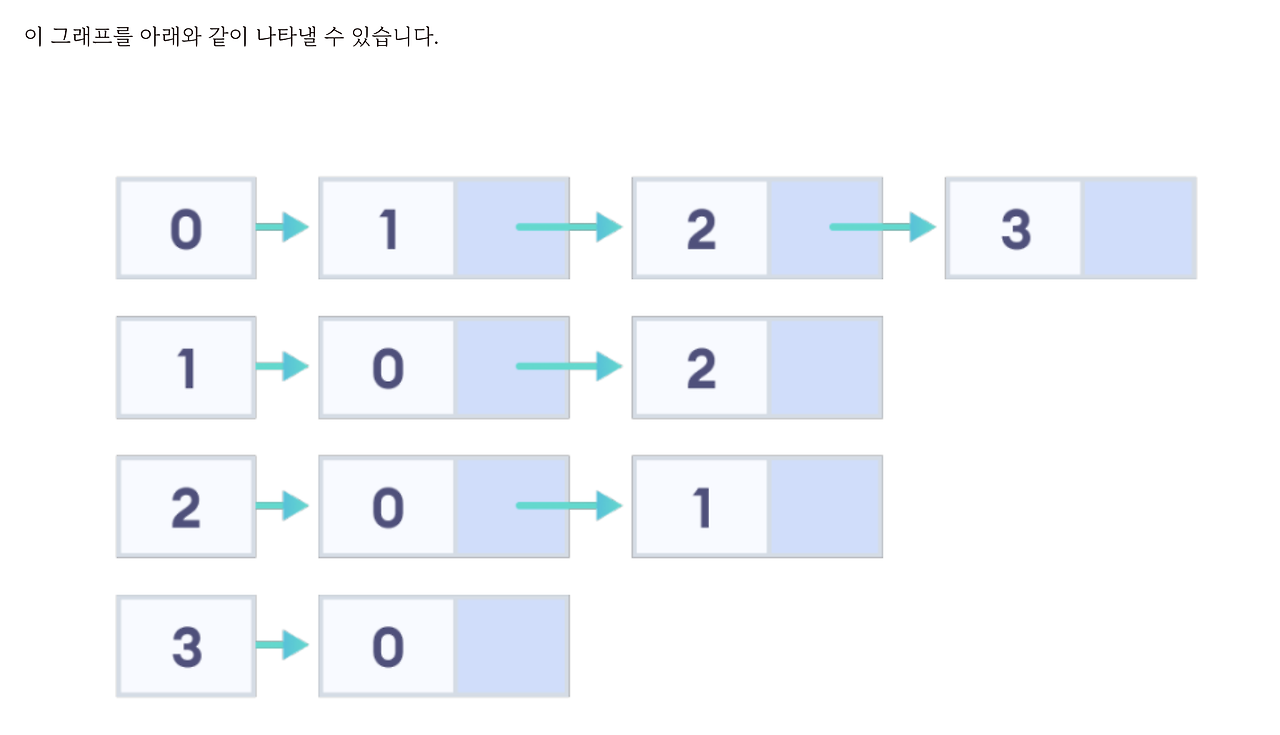
이런 식으로 각 정점마다 연결 리스트를 만들고 그 연결 리스트에 연결된 정점만 집어 넣는 거예요.
자 바로 코드를 보도록 하겠습니다.


자 일단은 4개의 정점이니까 이런 식으로 4개만큼 만들었죠.
'선생님 근데 연결리스트인데 왜 vector로 구현하나요?'

그냥 이렇게 하면, 연결 리스트가 하나밖에 없는 거죠.
인접리스트가 연결 리스트로 하는 건데 vector로도 구현을 할 수가 있어요.

보통은 연결리스트로 구현하면 이렇게 되는 거잖아요. 왜 연결 리스트가 아니라 vector로 구현해도 되는지는 제가 이따가 설명을 해드릴게요.
일단 여기에서 vector Adjacent가 여러 개가 있어요. 근데 여러분 정점마다 하나씩 만들어야 되는 거예요. 정점마다 Adjacent가 하나씩 있는 거예요.

그러니까 이렇게 해야하는 거예요. 이건 뭘 의미하냐면 vector가 여러 개 있는 거예요. 왜? 정점마다 연결리스트가 필요하니까. 그리고 연결리스트라고 설명을 했는데 구현은 vector로 구현할 수가 있다. 그거는 제가 이따가 설명을 드린다고 했어요.
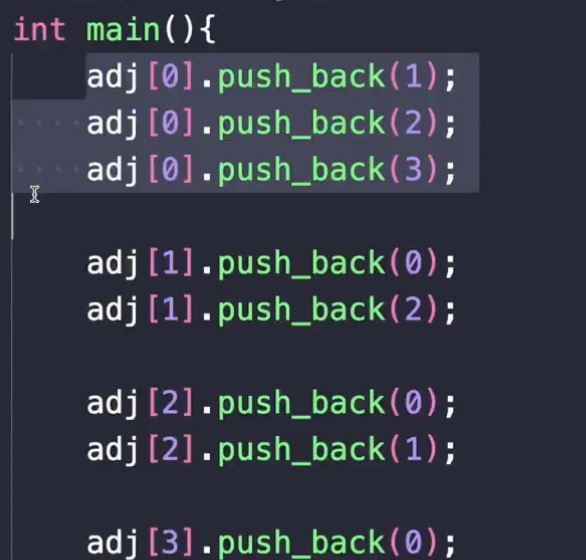
정점마다 연결된 거를 넣어줍니다. adj의 인덱스는 몇 번의 정점을 가리키는 거예요.
자, 이렇게 해서 4개 정점이니까 4개의 Adjacent vector 4개를 만든 거에요. 그렇게 해서 연결된 정점을 push_back 하고요.
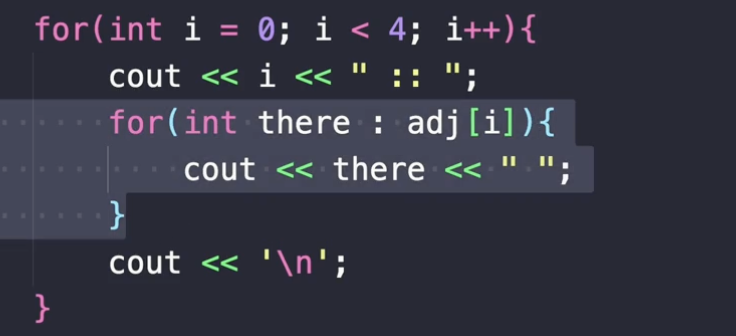
몇 번 정점에 연결된 것들을 이런 식으로 순회를 해서 연결된 정점을 뽑아내실 수가 있는 거에요. 지금 이거는 C++에서 제공하는 범위기반 for문인데
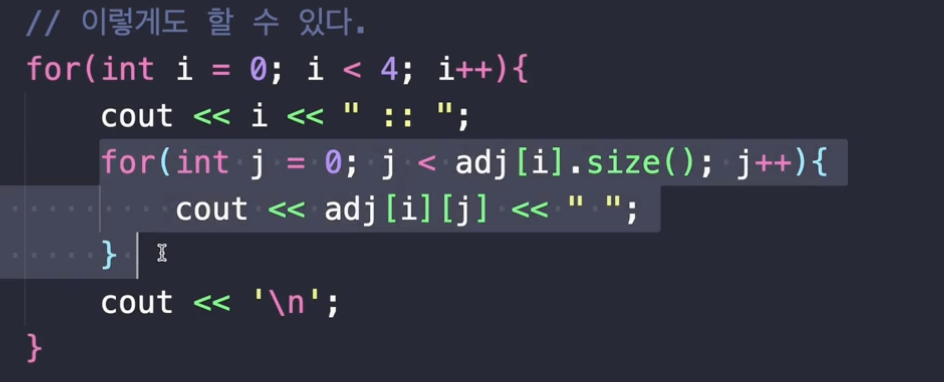
이거랑 같은 의미예요. 왜냐면 '몇 번은 뭐와 연결되어 있어, 어떤 정점과 연결된 정점은 뭐가 있어' 라고 했을 때 이런 식으로 하드코딩 할 수도 있죠. 이걸 컴파일 하시면
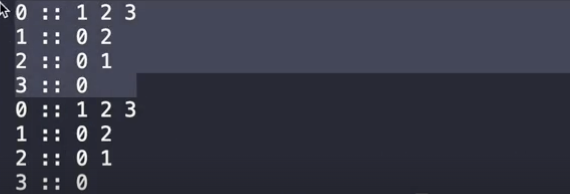
이렇게 잘 나타나는 것을 볼 수가 있죠.

근데 저희가 앞서서 설명은 연결리스트로 하고 왜 구현은 vector로 했을까요? 사실 둘 다 가능해요. 연결 리스트로도 할 수 있고 vector로도 할 수가 있는데 저는 편의상 벡터를 많이 씀니다. 이거는 연산의 시간 복잡도 차이 때문에 그래요.

연결 리스트는 n번째 인덱스 또는 마지막 요소의 삽입 삭제가 O(1)이고요 특정 요소, n번째 요소를 탐색하거나 참조하는데 O(n)이 걸려요.
여러분들이 연결 리스트라는 자료 구조를 생각을 하시면,

이런 것을 상상을 하시면 되게 편해요. 뭐냐면 상자 안에 요소가 있는 거예요. 상자를 까보기 전까지는 모르죠. 어떤 상자 안에 이러한 요소들이 있는데 까보기 전엔 몰라요.
연결 리스트에서 삽입과 삭제를 볼게요.

예를 들어서 여기다가 삽입을 하고 싶어요.

그러면 이 선을 끊고 이렇게 연결시키기만 하면 되는 거예요.
만약에 삭제를 하고 싶다. 라고 하면,
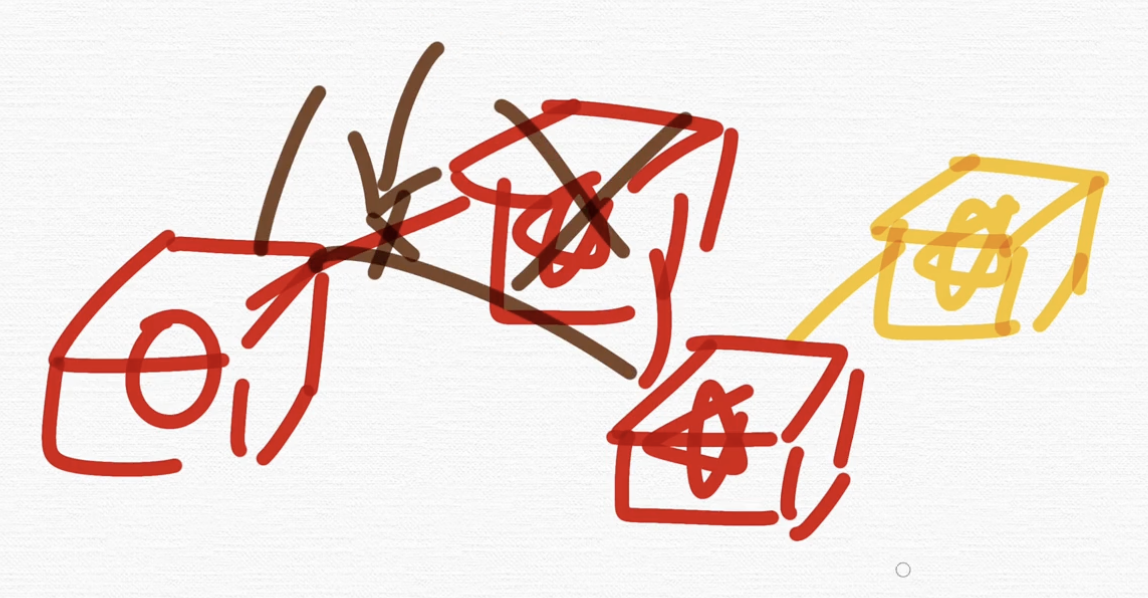
얘를 없애고 이렇게 연결시키기만 하면 되는 거죠.
그래서 이 연산이 되게 간단하기 때문에 삽입과 삭제에서는 n번째든 마지막 요소든 다 O(1)이 걸려요.
근데 예를 들어서 탐색을 한다고 해볼게요.

세 번째의 이 요소를 찾는다고 할게요.

그러면 이렇게 순차적인 탐색밖에 안 돼요. 상자를 까보면서 탐색을 해야 되기 때문에.
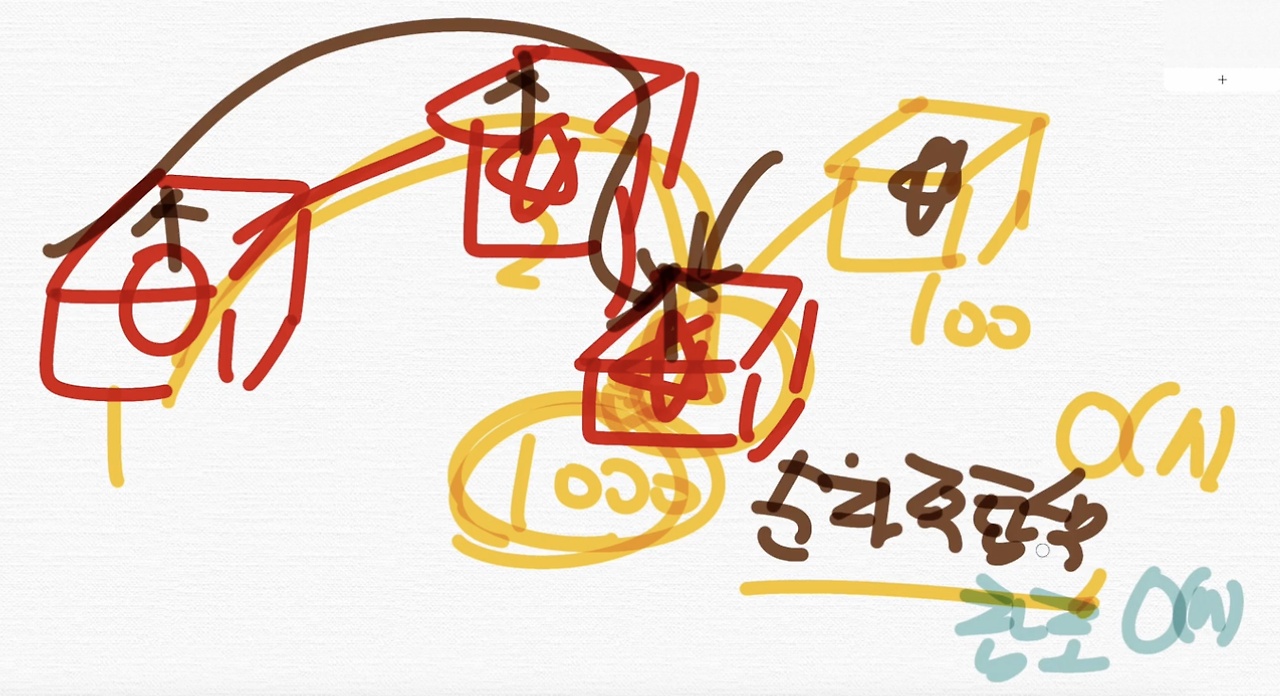
예를 들어서 이렇게 값이 1, 2, 1000, 100이 들어있다라고 해볼게요. 그럼 값이 1000임을 찾으려면 순차적인 탐색이 일어나야 되는 거예요. 그래서 탐색이 O(N)이 걸리고, 참조도 O(N)이 걸려요.

그러니까 연결 리스트는 배열처럼 이렇게 세 번째 요소, 두번째 요소 이렇게 바로 참조가 불가능해요. 그래서 참조도 순차적 참조밖에 안되고, 탐색도 순차적 탐색밖에 안돼요.
그래서 이 두 가지 연산 자체가 O(N)이라는 시간 복잡도를 가지는 거에요.
반면 vector를 볼게요.

자 여러분 vector는 이렇게 생각하시면 돼요.

상자 위에 요소가 있고 연속된 메모리 공간에 이렇게 있는 거예요. 얘는 까져있는 초콜릿 상자죠.
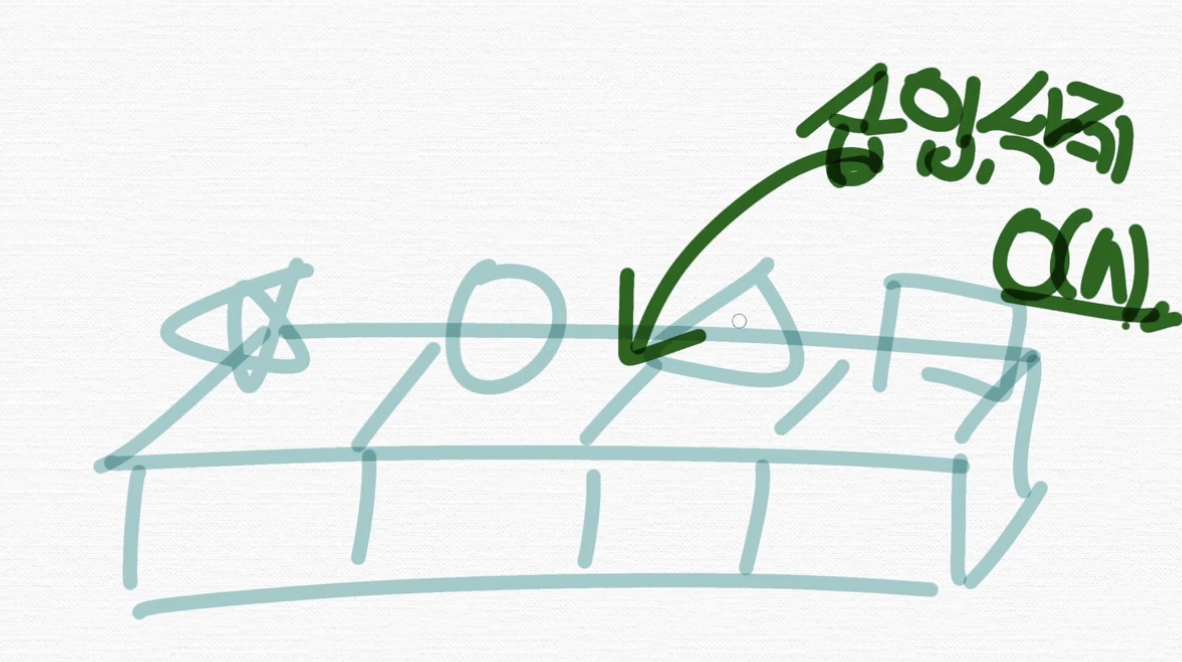
여기서 만약에 n번째, 이 부분에다가 어떤 요소를 삽입하려면 메모리 복사 등등이 필요해서 삽입, 삭제 같은 경우는 O(N)이 걸려요. 이건 좀 오래 걸리지만,
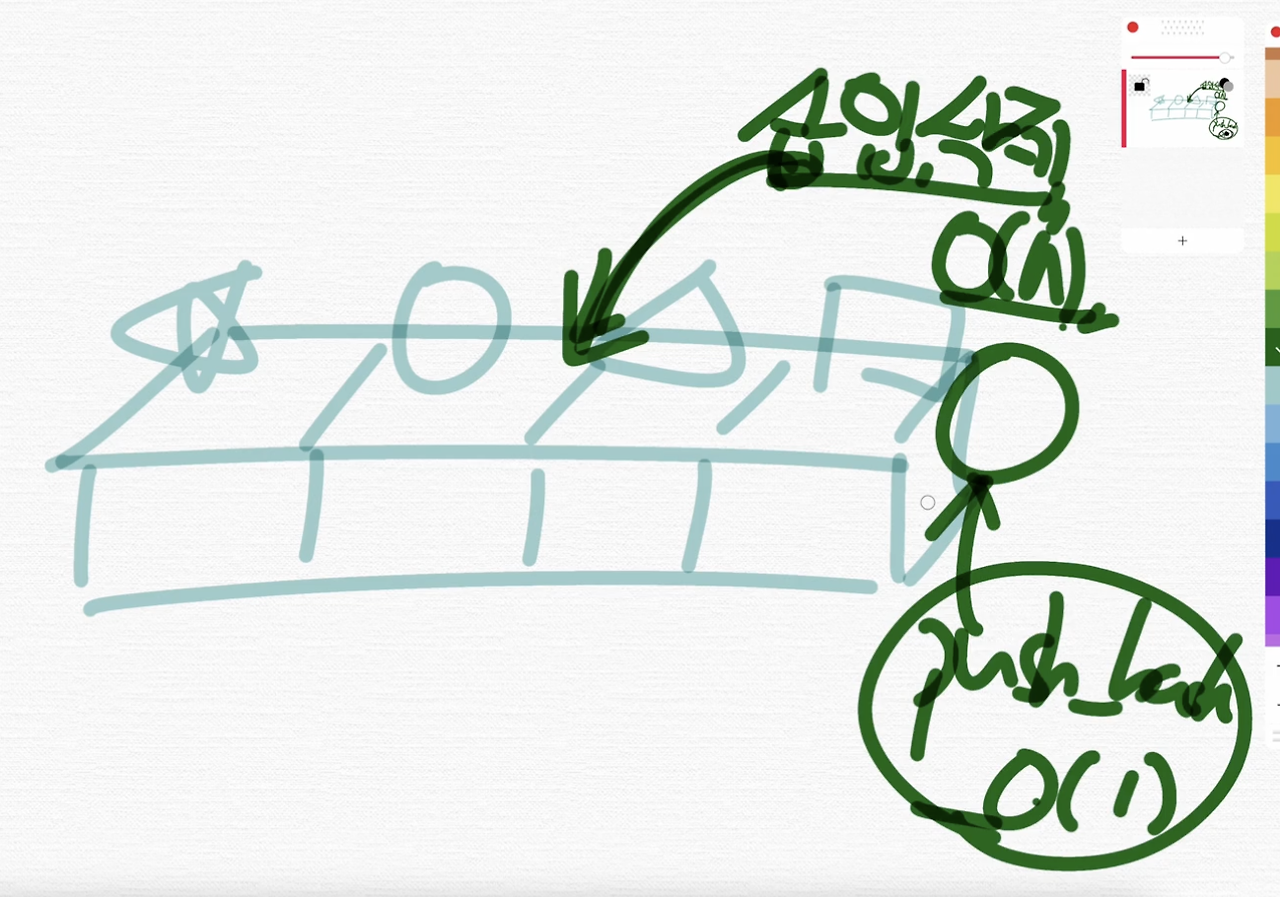
마지막 요소에 push_back 하는 건 O(1)이 걸리거든요.
이거는 push_back을 할 때마다 크기가 2배, 2배 log 함수처럼 증가해서 그런 건데 이건 조금 복잡한 개념이라서, 일단은 그냥 마지막 요소에 삽입 삭제가 O(1)이다. 라고 보시면 되고요.
그리고 특정 요소의 탐색과 참조가 O(N), O(1)예요.
예를 들어서 '세모라는 값을 찾고 싶어!' 라고 했을 때 vector도 배열과 동일하게
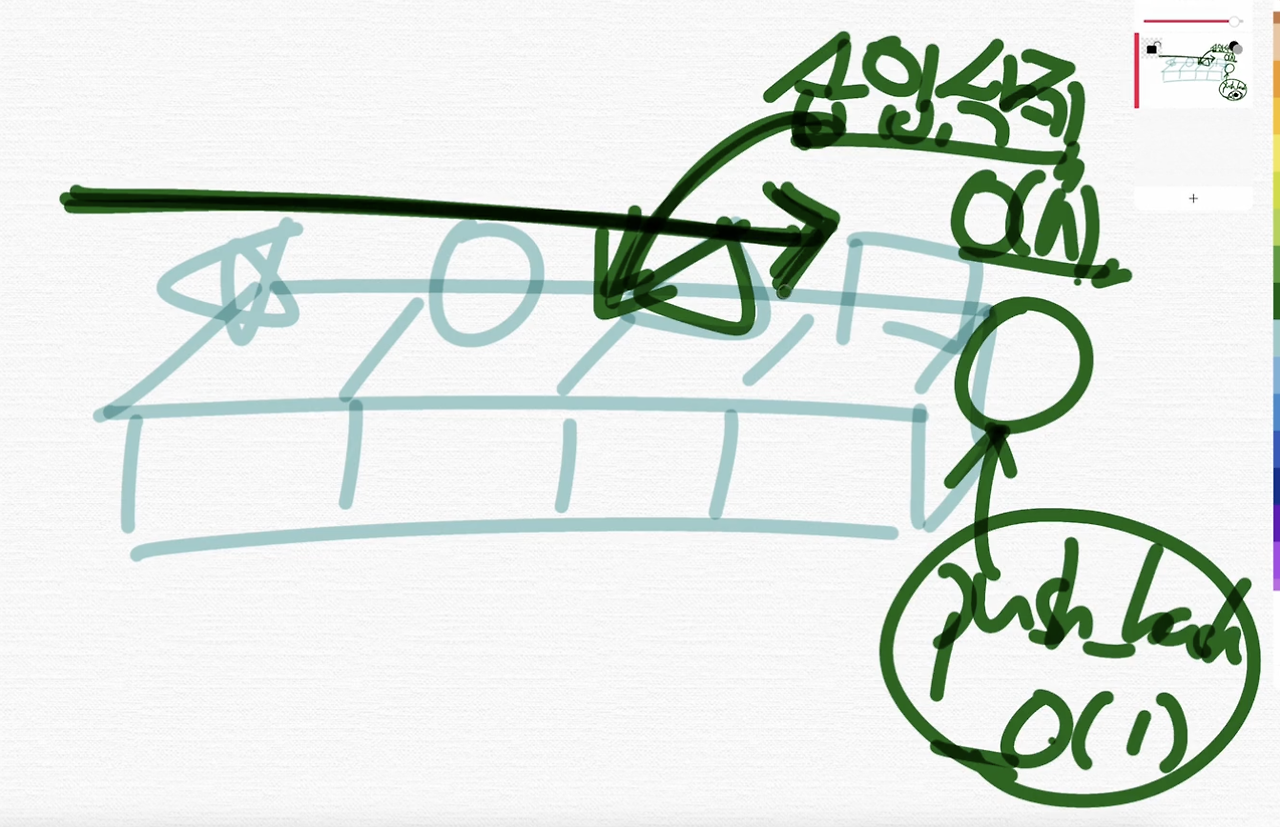
이런 식으로 순차적으로 탐색할 수 밖에 없어요.
그런데 참조는 O(1)이 걸려요. 그러니까 vector는 Random access가 가능해서,

이런 식으로 []로 몇 번째의 요소에 대한 참조가 가능해요. 연결리스트는 이런 게 불가능하고요.
이런 차이가 있는 거예요.
그런데 우리가 앞서서 봤던 코드를 잠깐 보면

여기서 어떤 코드가 많이 나오죠? push_back 이랑 순회하면서 탐색하는 게 나오죠.
우리가 인접 리스트를 구현했을 때 많이 사용하는 로직을 보면 push_back이랑 탐색 로직인데,

연결리스트로 구현하든, vector로 구현하든 시간 복잡도는 동일하니까 그냥 우리에게 더 익숙한 vector를 쓰는 거예요. 그리고 n번째 요소 참조에서 vector가 더 빠르기 때문에 쓰는 것도 있습니다.

그래서 인접리스트를 구현한다고 했을 때 인접 리스트는 연결 리스트를 기반으로 구현하는 거다 라고 생각을 하시고, 코드 베이스로 구현할 때는 vector로 구현하는 것을 추천을 드립니다.
그럼 또 퀴즈를 풀어볼까요?

질문을 하면 여러분들이 어떻게 구현할까라고 생각을 좀 하셔야 돼요. 생각을 했다 칩시다.
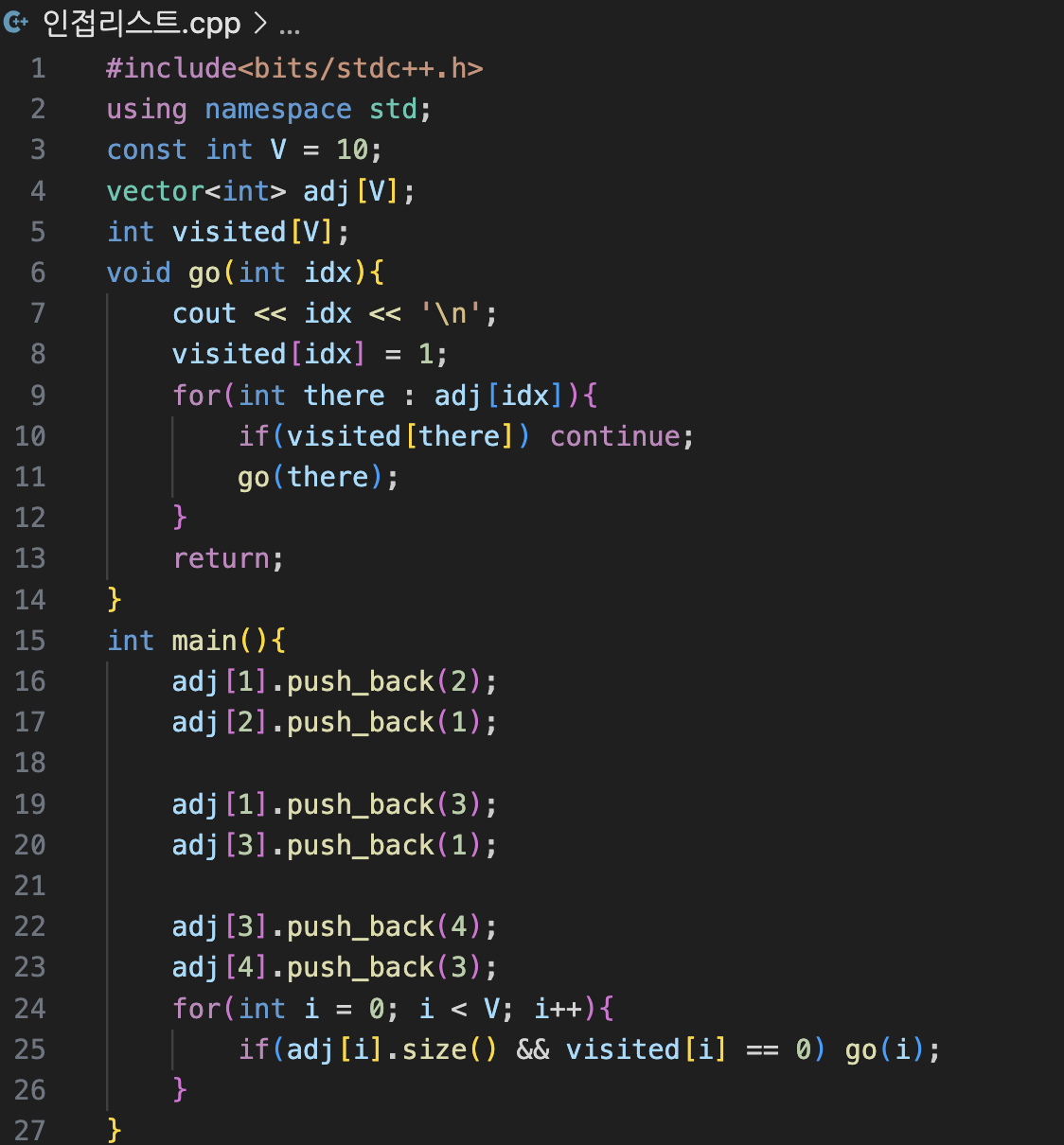
정답은 이거예요. 보도록 할게요.

일단은 양방향에서 만들죠.
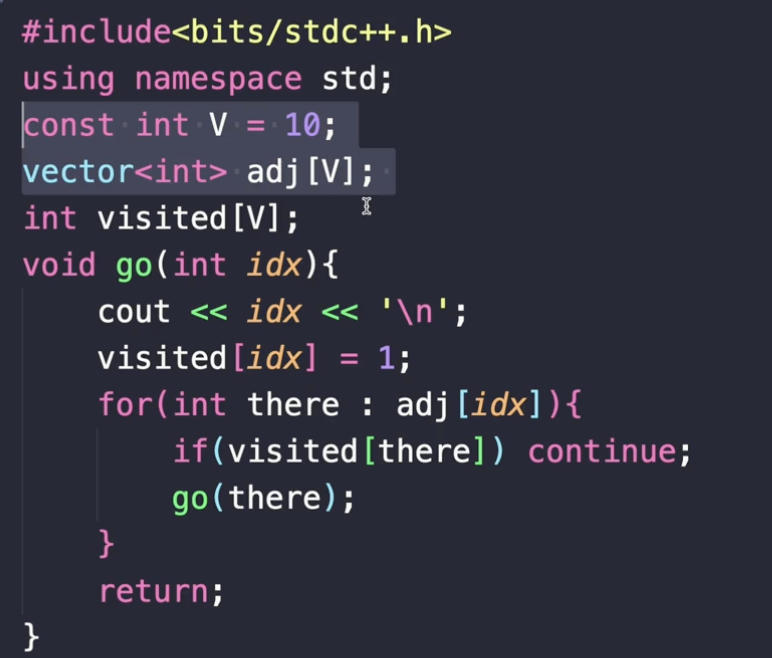
정점은 10개니까 10개만큼 만들어야겠죠. 방문했다면 방문하지 않게끔 하려고 인접행렬과 동일하게 만들었습니다.
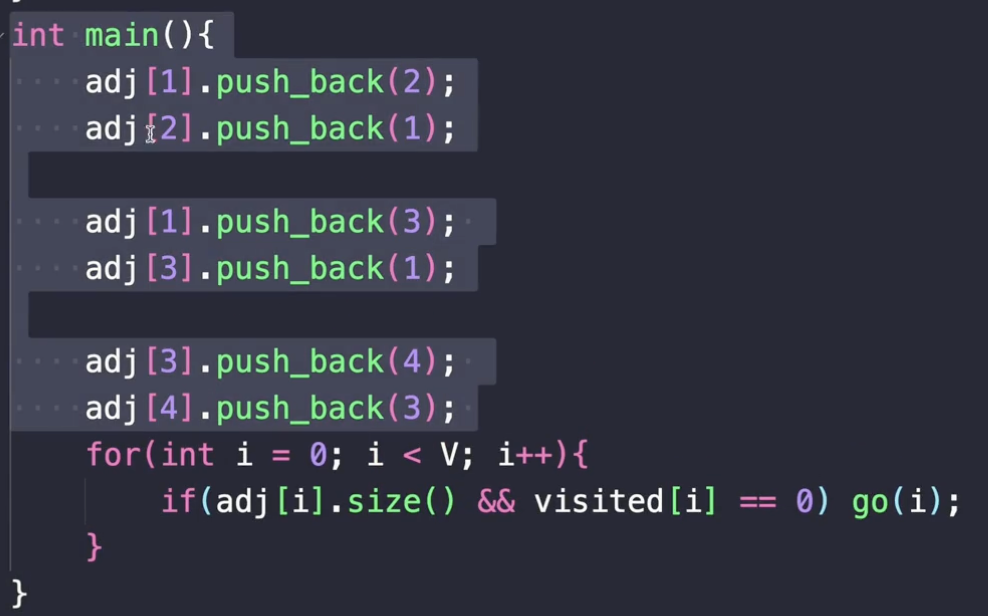
이렇게 push_back을 해서 인접 리스트를 만들었어요. if 문을 보면, 만약에 연결되어 있는 정점이 있고, 해당 정점을 방문하지 않았다면 go 라는 재귀함수가 작동이 됩니다.

go 함수 안에는 출력하는 로직이 들어있죠. 그리고 순회하면서 만약에 연결되어 있는 정점이 이전에 방문 되었다면 continue 하고, 아니라면 go를 다시 들어가죠.
그러니까 뭐냐면 자, 제가 그림을 통해서 볼게요.

이렇게 해서 1, 2, 3, 4가 출력이 될 겁니다. 출력을 해보면,

잘 나오는 걸 볼 수 있죠.
이렇게 인접 리스트에 대해서 얘기를 해봤습니다.
'스터디 인증' 카테고리의 다른 글
| 2주차 개념 #7. 맵과 방향벡터(direction vector) (0) | 2024.03.24 |
|---|---|
| 2주차 개념 #6. 인접행렬과 인접리스트의 차이 (0) | 2024.03.21 |
| 2주차 개념 #4-2. 인접행렬(adjacency matrix) (0) | 2024.03.19 |
| 2주차 개념 #4-1. 인접행렬(adjacency matrix) (0) | 2024.03.19 |
| 2주차 개념 #3. 이진트리와 이진탐색트리 (0) | 2024.03.18 |




