당니의 개발자 스토리
2주차 개념 #4-2. 인접행렬(adjacency matrix) 본문
2주차 개념 #4-2. 인접행렬(adjacency matrix)
문제를 풀어보면서 배워보도록 할게요.

한번 생각해본 다음에 답을 보셔야 합니다.

쉽죠?

이건 뭘까요?

간단하죠? 연결되어 있다, 인접해 있다 이걸 그냥 1 또는 0 이렇게 표현하는 거예요.

이건 뭘까요?

이렇게 만들어야 겠죠. 물론 20보다 큰 수를 담을 수가 있어요. 뭐냐면 정점의 개수가 20개가 있으면,

이렇게 해도 할 수가 있어요. 그러니까 20개 이상이면 되는 거예요.
우리가 표현해야 되는 건 뭐? 정점의 개수가 20개일 때,
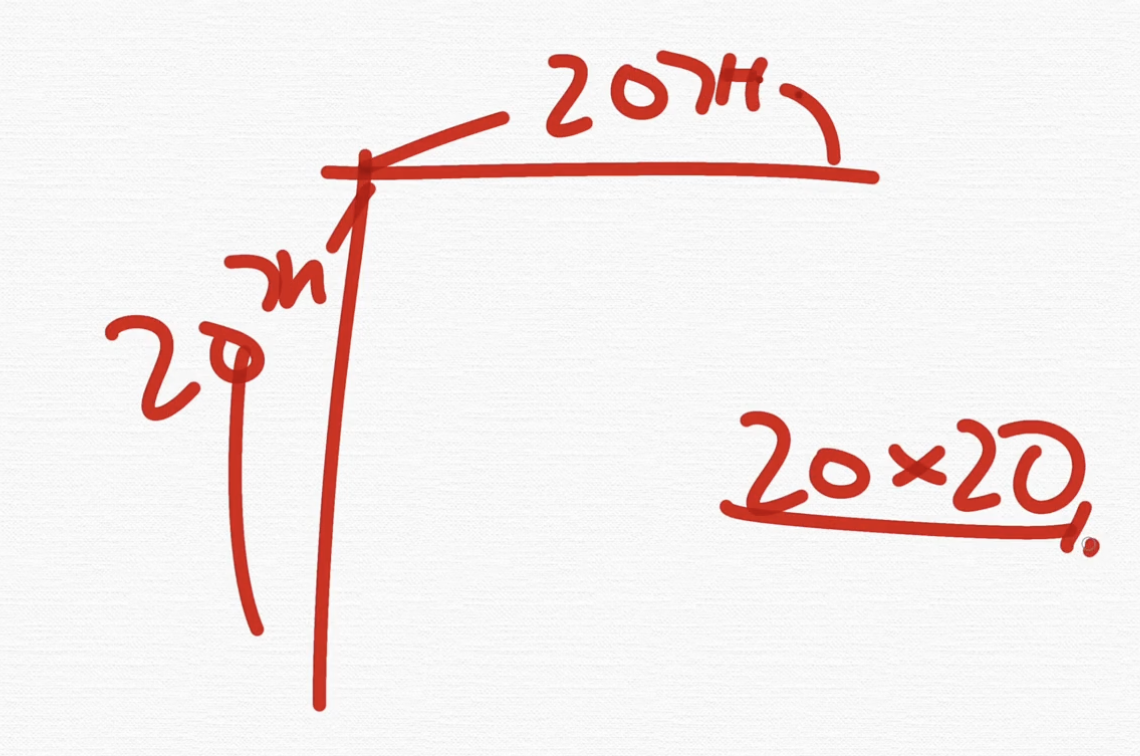
이렇게 2차원 배열이 필요한 거예요. 20개 곱하기 20개가 필요한데, 사실은 이것보다 조금 더 큰 값을 부여할 수 있다는 소리예요. 근데 문제는 메모리를 최소화해야 된다고 했기 때문에 20 곱하기 20 배열이 필요하다는 겁니다.
그럼 이제 마지막 문제를 풀어보고 인접행렬에 대한 설명을 마치도록 하겠습니다.
1번과 2번에 대한 지문을 보고 생각해 보시고 풀어 보세요.

이것에 대해서 여러분들이 생각을 하시고 풀어보세요. 그러니까 무방향 그래프예요. 양방향 간선이다라는 거예요.
이 두가지를 충족하는 코드를 여러분들이 구현을 해보시는 거예요.
자 조금 더 그림을 그려가면서 해보도록 할게요.

이런 그래프에서 첫 번째, 0번부터 탐색하는 로직을 만든다는 거예요.
두 번째는 방문한 정점은 다시 방문하지 않는다는 거예요.
이런 탐색이 또 처음이기 때문에 어려울 수 있는데 생각이 틀려도 괜찮아요.
어떻게 하면 방문한 정점은 다시 방문하지 않을 수 있을까?

충분히 손코딩을 하시고 정답코드를 보시면 됩니다.
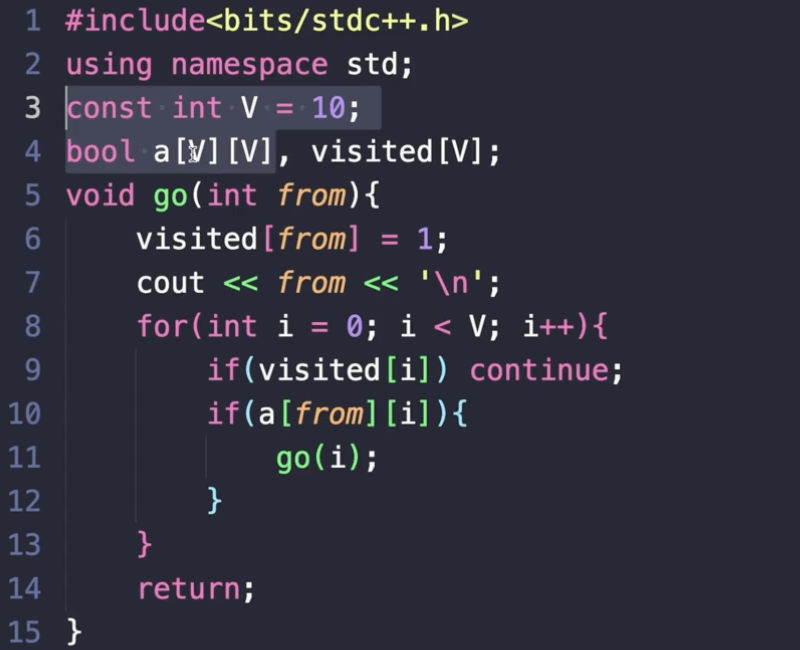
일단은 인접행렬을 정의를 해야 되겠죠? 10개니까 boolean 정사각형 행렬을 이렇게 정의를 했어요.
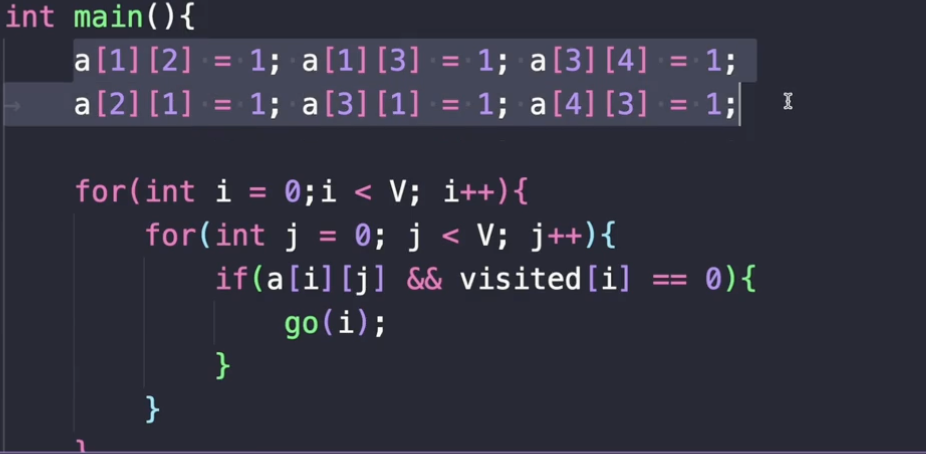
그리고 양방향 간선이니까 거기에 해당하는 표기를 했죠?
그리고 0번부터 방문 안한 노드를 찾는다고 했죠?
근데 이런 인접행렬을 한다고 했을 때,

이런 식으로 이중 for문을 통해서 한다고 했죠. 이렇게 해가지고 만약에 i부터 j까지 연결되어 있고, visited[i]가 0이라면 방문을 안 한거예요.
잠깐 visited가 왜 나왔냐면 방문한 정점은 다시 방문하지 않는다고 했죠. 이거를 구현하려고 제가 visited 라는 배열을 생각한 거예요.

그림에서 방문한 정점은 초록색으로 색칠해볼게요.

그런데 2번으로 갔다가 다시 1번으로 가려고 할 수도 있겠죠.
근데 제가 초록색으로 색칠한 거는 다시 방문하지 않는다는 규칙을 만든 거예요.
이걸 코드로 나타내면,

visited 라는 배열을 만들어서 방문했다면 visited 라는 배열의 해당 정점에 대하여 1이라고 표기를 하는거죠. 그럼 'visited[i]이 1이구나' 해서 아 여기는 이미 방문했구나 라고 인지하게끔 하는 거예요.
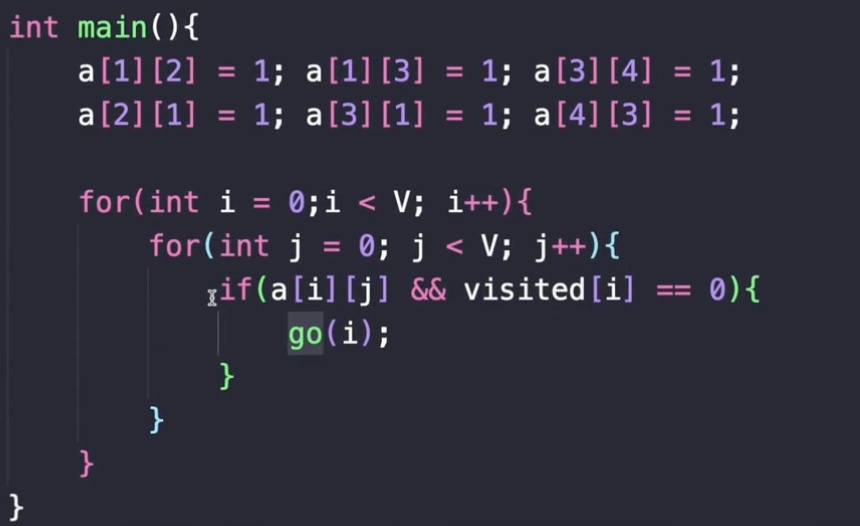
그래서 visited 라는 배열이 필요하다는 거고, 이제 go 라는 함수를 볼게요.
일단 i부터 j까지 가는 간선이 있고요. 그리고 해당 정점이 방문하지 않았을 경우에는 go 라는 재귀함수가 작동되게 됩니다.
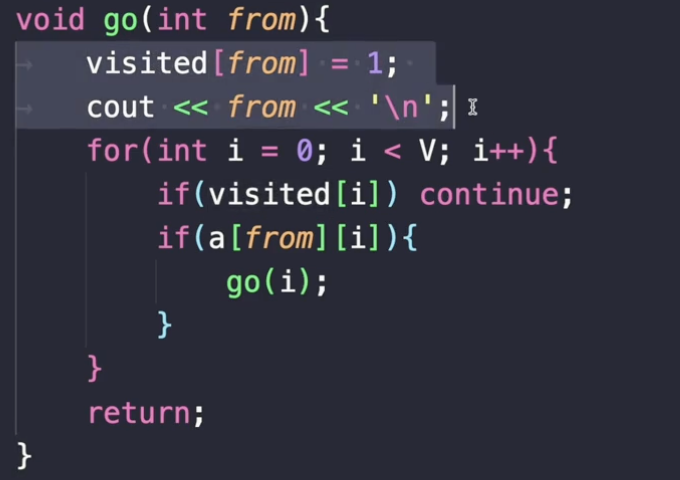
이 go 라는 함수를 보시면, 방문 처리하면서 방문한 곳이 어디인지 출력하고 있죠.
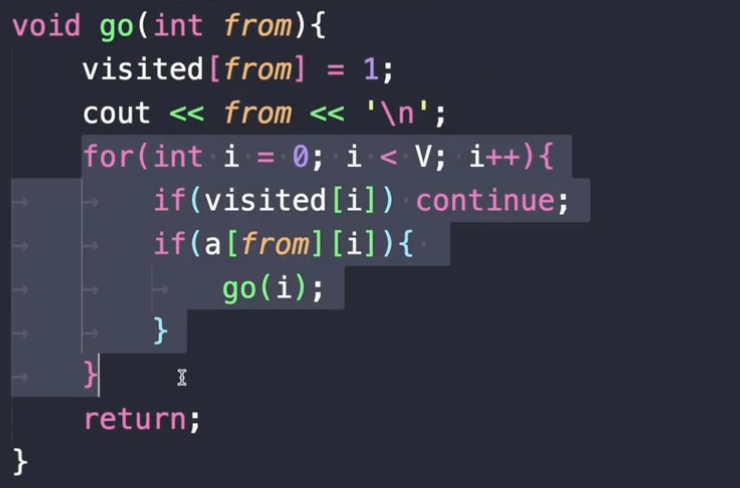
그리고 나서 이 정점과 연결되는 정점을 찾는 거죠.
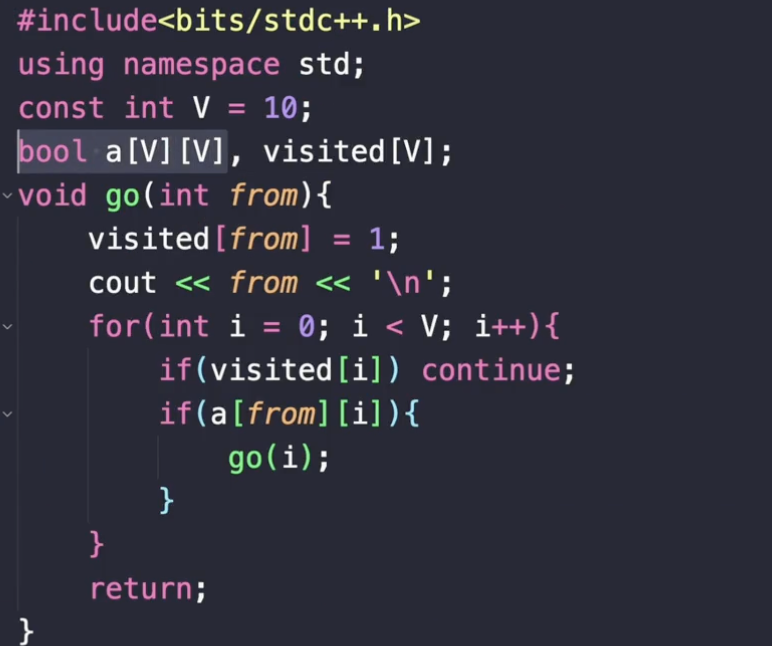
이렇게 해서 인접행렬, vertex 곱하기 vertex인 2차원 배열이 필요한 거예요.
그래서 출력을 해보면,

1, 2, 3, 4 잘 나오는 걸 볼 수 있습니다.
이렇게 해서 인접행렬에 대해서 알아봤습니다.
'스터디 인증' 카테고리의 다른 글
| 2주차 개념 #6. 인접행렬과 인접리스트의 차이 (0) | 2024.03.21 |
|---|---|
| 2주차 개념 #5. 인접리스트(adjacency list) (0) | 2024.03.20 |
| 2주차 개념 #4-1. 인접행렬(adjacency matrix) (0) | 2024.03.19 |
| 2주차 개념 #3. 이진트리와 이진탐색트리 (0) | 2024.03.18 |
| 2주차 개념 #2. 트리(Tree Data Structure) (0) | 2024.03.18 |




