당니의 개발자 스토리
Linear Regression 본문

손실함수를 Mean-Squared Error 라고 하고 내 모델의 예측값과 정답 간 차이의 제곱을 비교하는 형태로 Loss를 계산하고,
이 손실이 가장 작아지도록 하는, 즉 내 모델과 정답의 오차가 가장 적은 a와 b를 찾는 문제가 선형회귀 문제였음.
우리가 바라보게 될 Supervised Learning 문제들은 실제로 다차원인 경우가 많음.
그림 같은 경우도 다차원 벡터임
문제 같은 경우도 우리가 벡터로 Embedding 하게 된다면 굉장히 다차원 형태의 입력이 될 것임
그래서 수업에서는 다차원 입력에 대한 Linear regression을 다룰 것임

이번엔 "키"와 "손 크기(hand size)" 두 가지 정보를 가지고 몸무게를 예측한다고 생각
x = (x₁, x₂)에서
- x₁: 키
- x₂: 손 크기
모델
- y = a₁x₁ + a₂x₂ + b
→ 키와 손 크기가 클수록 몸무게도 클 거라고 예측하는 모델
손실 함수
- 마찬가지로 ((a₁x₁ + a₂x₂ + b) - y)^2
→ 예측값과 실제 몸무게의 차이 제곱
그렇다면 변수가 세 개이면 어떻게 될까?

3개의 데이터 샘플이 있을 때, 각 샘플의 오차 제곱을 모두 더하고 평균을 낸 형태예요.
그리고 이걸 전개해 보면 기울기(a₁, a₂)와 절편(b)에 대해 이차 함수(quadratic function)가 됨
이차 함수는 볼록한 형태여서 최소값이 하나 존재하고, 그걸 찾으면 최적의 직선을 알 수 있음
우리가 후에 Gradient Descent를 설명할 때, a1에 대해서 미분하고, a2에 대해서 미분하고, b에 대해서 미분한 함수
Gradient(기울기)는 결국에는 어느 방향으로 가장 빠르게 증가하는가를 나타내는 지표라고 보면 된다.
왜 기울기를 구하나요?
- 기울기 = 미분 결과
→ 손실 함수가 가장 작아지는 지점을 찾기 위해서
각각의 변수에 대한 편미분
- ∂L/∂a₁: a₁ (키에 대한 영향력) 변경 시 손실이 어떻게 변하는지
- ∂L/∂a₂: a₂ (손 크기에 대한 영향력)
- ∂L/∂b: b (절편)
→ 이 미분값들을 0으로 두고 풀면 가장 좋은 선형 모델을 구할 수 있음.
손실 최소화와 경사 하강법
목적
- 손실함수 L(a)를 최소화
- 즉, 모든 데이터에서 예측값과 실제값의 차이를 제곱한 것들의 평균을 최소로!
경사하강법(Gradient Descent)
- 손실을 줄이기 위해 a를 조금씩 바꾸는 알고리즘입니다.
- 수식:
∇L(a) = (1/n) ∑ ∇(예측값 - 실제값)^2

변수가 늘어나도 걱정하지 않아도 됨. 어차피 1차식으로 나온다.
이 3개의 식을 풀면 언제 L이 가장 작아지는지 알 수 있음.

d차원으로 두려움 없이 넘어가자!
- 입력이 키, 손 크기, 나이, 체지방률, 팔 길이 등등 많아질 수 있음
- 그럼 입력 벡터 x = (x₁, x₂, ..., x_d)이고
모델은 y = aᵀx + b로 표현됩니다. → aᵀx는 a와 x의 내적(dot product)
절편 b를 포함한 표현 (x₀ = 1)
왜 이렇게 바꿀까?
- y = aᵀx + b를 하나의 점곱으로 처리하기 위해
→ x₀ = 1을 도입해서 x = (1, x₁, ..., x_d)로 확장
→ a = (b, a₁, ..., a_d)로 확장하면 식이 y = aᵀx로 정리

변수가 d+1 개이고, L(a)를 찾기 위해서 이 d+1 개에 대해서 각각 미분해보면
d+1 개의 변수와 d+1 개의 식으로 이루어져 있는 문제를 푸는 것인데, 수학적인 툴들을 사용해서 이 문제를 아름답게 풀어보겠다.

- 데이터가 여러 개 :
키, 손 크기, 나이 등 여러 특징(x)을 보고 몸무게(y)를 예측하려는 상황입니다. - 데이터 개수: n개
- 특징 개수: d개
X는 각 행이 하나의 데이터(예: 사람 1명)의 특징 벡터(x₁, x₂, ..., x_d)
Y는 각 데이터에 대해 알고 있는 실제 몸무게
손실 함수 (Loss Function)
- Xa: 우리가 예측한 값들 (n개)
- Y: 실제 값들 (n개)
- 둘의 차이의 제곱합을 최소화
전개하면 L(a) = aᵀXᵀXa - 2YᵀXa + YᵀY
→ 미분하기 쉽게 바꾼 형태

미분해서 최소값 구하기 -> ∂L/∂a = -2XᵀY + 2XᵀXa = 0
정리하면, XᵀXa = XᵀY
→ 이게 Normal Equation (정규 방정식)
d+1개의 변수를 연립방정식으로 푸는 것보다 훨씬 깔끔하게 풀 수 있음
기울기 a = (XᵀX)⁻¹ XᵀY
→ 이게 바로 선형 회귀 해석적 해답.
→ 역행렬을 통해 a를 한 번에 계산할 수 있음

파란색 점(데이터)들을 보면 직선으로 표현하기에는 무리가 있음.
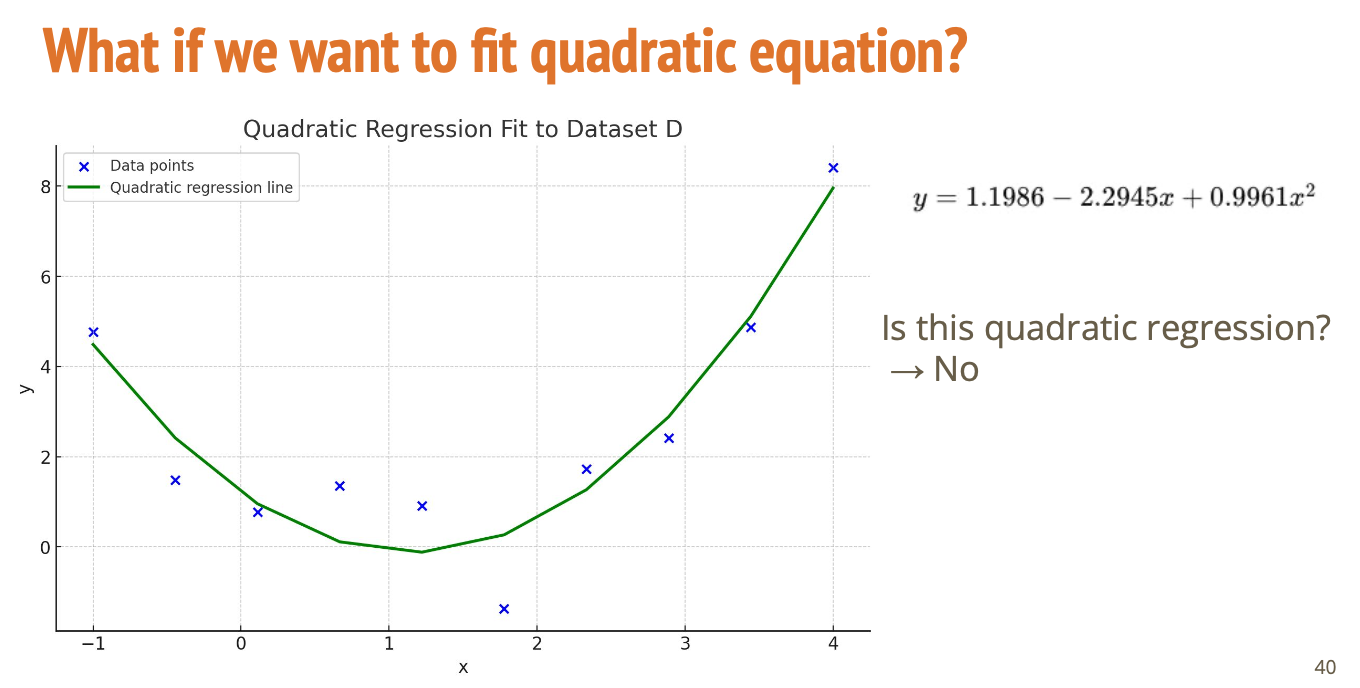
y = a·x² + b·x + c
- 이차 함수로 데이터를 맞추면
→ 데이터의 패턴을 더 잘 따라감 - 초록 선은 이차 회귀 결과
그럼 이건 선형 회귀가 아니고 이차 함수니까 이차 회귀겠네? -> NO🙅🏻♀️
x에 대한 이차식으로 y를 표현하는 문제가 되었지만, 우리가 해결하고자 하는 문제는 x와 y를 푸는 것이 아니라
x와 y는 주어진 것이고, x를 가지고 y를 표현할 때 x에 붙는 계수들, 즉 a0, a1, a2를 맞추는 문제이다.
그리고 이 수식 역시 a에 대한 일차식이 여전히 유지되기 때문에 '여전히 선형 회귀'로 볼 수 있음
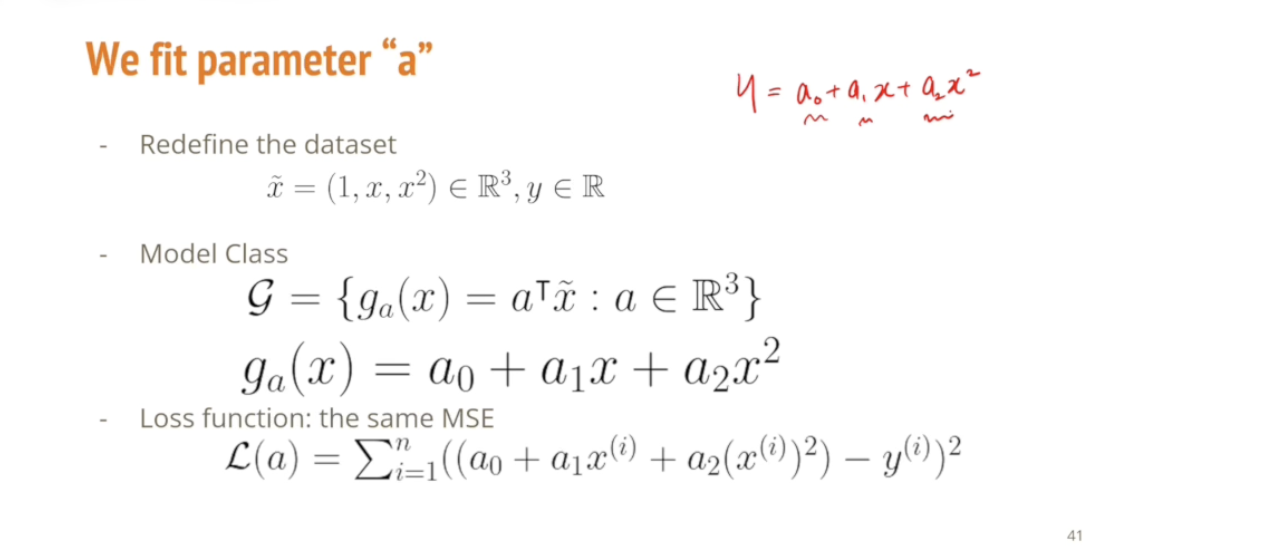
이 a0, a1, a2 에 대한 일차식, 선형함수는 여전하기 때문에 이 문제 역시도 선형 회귀로 풀도록 하자.

아까 일차보다 이차함수를 도입했더니 더 좋은 결과가 나왔으니, 더 높은 차수, 지수함수 등과 같은 추가 함수를 넣어서 보다 복잡한 형태의 함수로 더 완벽하게 설명하고자 하는 욕구가 들 수도 있음.
그래서 이러한 더 높은 차수, 지수함수와 같은 형태의 피처, 혹은 커널들을 추가하는 형태로 더 표현력이 높은 함수를 구현할 수 있음.
이렇게 되면 필연적으로 Overfitting 이라는 문제에 봉착하게 됨
왜 이러한 문제가 발생하는지 나중에 설명함. 그런데 아까봤던 것처럼 적절하게 일차식에서 이차식으로 넘어가는 형태는 올바른 형태의 방향이라고 할 수 있음.
그래서 아까처럼 데이터를 직접 검사하거나 해당 데이터에 대한 전문지식이 있는 분들이 이 데이터를 가장 잘 표현하는 일련의 이론적 근거에 기반한 피처를 뽑아내는 것들은 권장함

파란 점: 원래 데이터 D (키 170 입력)
초록 점: 살짝 바뀐 데이터 D′ (잘못 입력했다! 180 으로 변경)
빨간 선: D에 대해 만든 직선
주황 선: D′에 대해 만든 직선
두 직선이 거의 겹침
즉, 데이터가 조금 바뀌어도 결과(직선)가 크게 변하지 않음
그러면 이제 내가 데이터를 더 잘 표현하겠다고 7차식으로 표현하는 경우에 비슷한 문제가 발생할 때 어떤 일이 일어나는지 살펴보자.
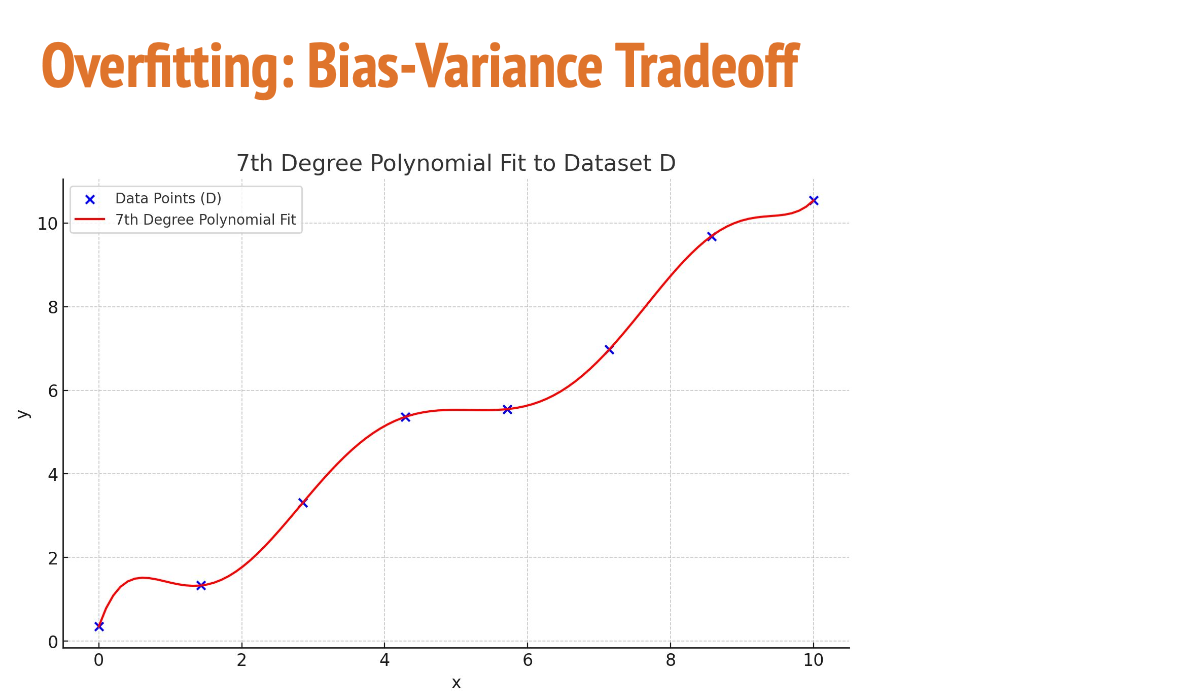
오버피팅(과적합)이 일어남.
지금은 훈련 데이터에는 정확하지만, 새로운 데이터가 들어오면 휘어진 부분이 엉뚱한 예측을 할 수 있음
즉, 너무 복잡하게 외워서 일반화가 안 되는 상황이 일어날 수 있다.

이것이 High Variance (높은 분산)
모델이 너무 민감해서 조금만 변화에도 예측이 바뀌는 불안정한 상태
Bias-Variance Tradeoff
| 선형 모델 (직선) | 단순하지만 안정적 | ↑ (높음) | ↓ (낮음) |
| 고차 다항식 | 복잡해서 훈련 데이터는 잘 맞춤 | ↓ (낮음) | ↑ (높음) |
결국 머신러닝에서 중요한 건 적당히 복잡한 모델을 찾는 것
→ 너무 단순하면 underfitting, 너무 복잡하면 overfitting이 발생함.
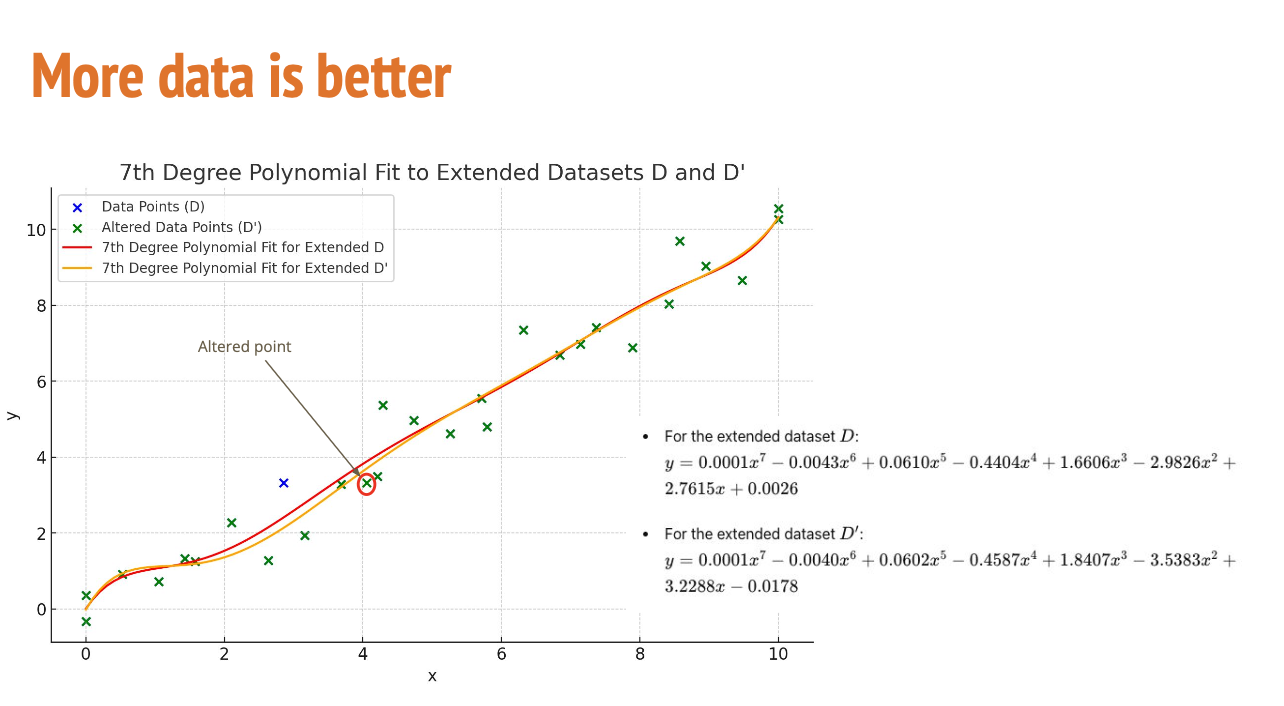
이런 문제를 푸는 가장 효과적인 방법은 데이터를 많이 주는 것.
실제로는 데이터가 굉장히 많이 주어진다는 보장이 없고 데이터가 부족한 경우 데이터를 더 많이 얻는 것은 대부분 비싸고 불가능한 경우가 많기 때문에
우리가 언제나 주어진 데이터 대비 모델이 너무 복잡하지 않은가?
내 모델의 복잡도 대비 데이터는 충분히 확보되어 있는가? 를 반드시 조심하는 것이 중요함
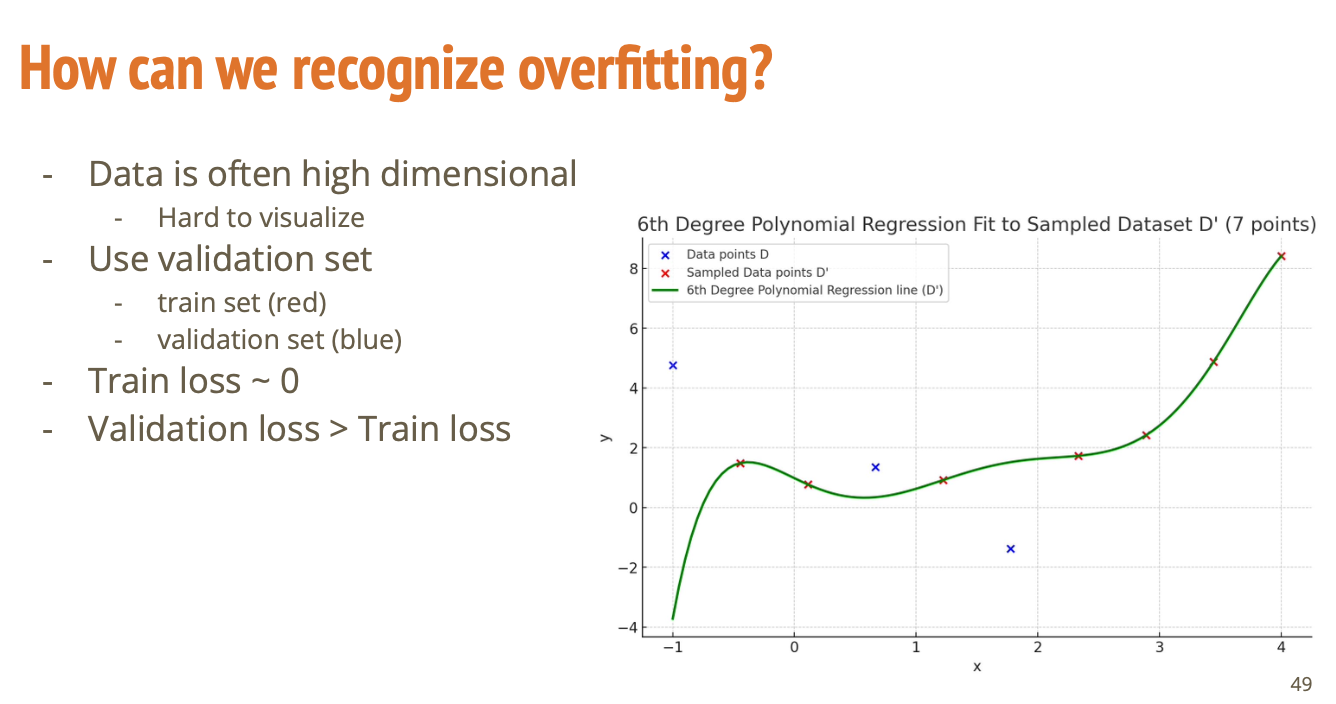
빨간색 점들 7개의 데이터만 사용하는 경우를 생각해보자. 그랬을 때 범용적으로 잘 적용이 되고, 데이터에 특별하게 오버피팅이 되어있지 않다고 한다면 이 일곱 개의 데이터를 가지고 계산하는 손실과 내가 train에 사용하지 않았던 데이터에 적용하는 손실 값의 간극이 그렇게 크지 않을 것이다.
- Train Loss ≈ 0
- 훈련 데이터는 거의 완벽하게 맞춤
- 그래프에서 빨간 점(Train)은 초록 곡선이 잘 지나감
- Validation Loss ≫ Train Loss
- 검증 데이터(파란 점)는 모델이 잘 예측 못함
- 검증 성능이 떨어짐 → 일반화가 안 됨
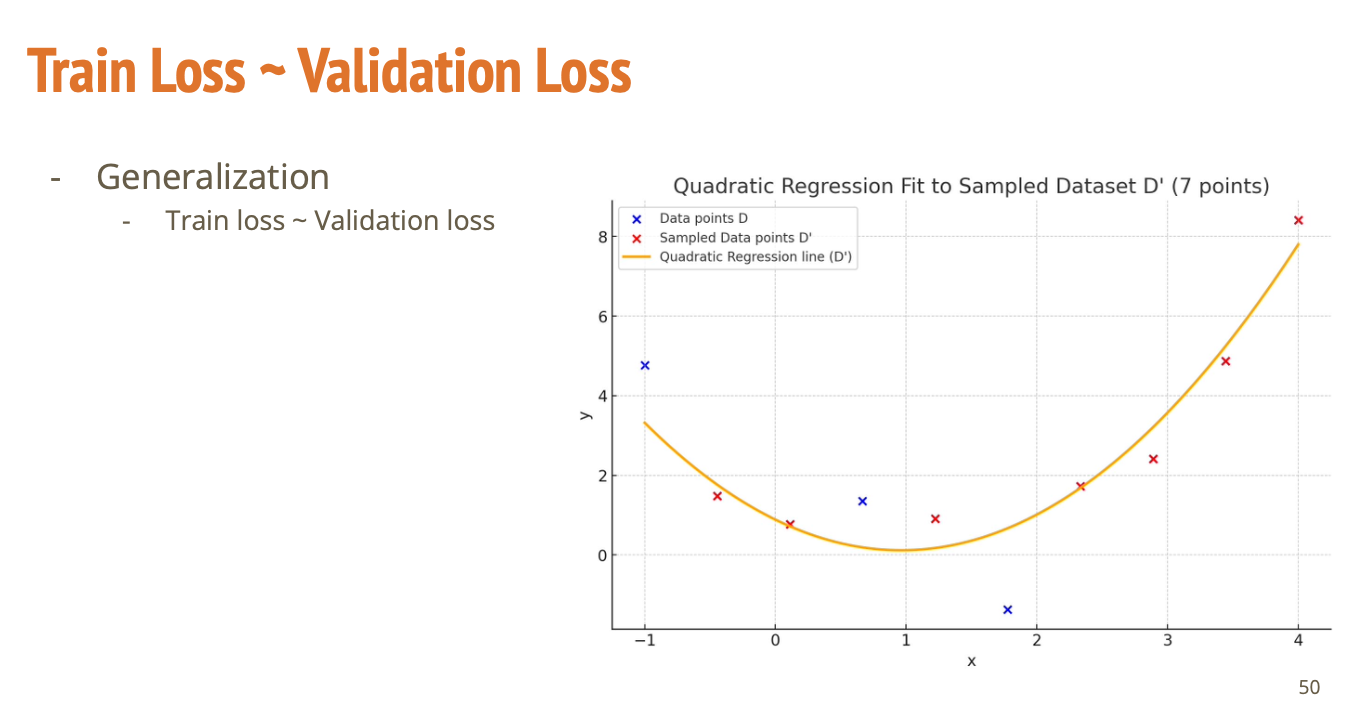
좋은 모델은 Train과 Validation의 성능이 비슷함
Train loss ≈ Validation loss
→ 빨간 점(Train), 파란 점(Validation) 모두 잘 맞는 곡선
과적합이 안 되고 새로운 데이터를 만나도 잘 작동할 가능성이 높음 -> 일반화 가능성 높음
데이터를 훈련 데이터와 검증용 데이터를 나눠서 평가하자!

데이터 종류 사용 목적 보통 비율
| Train Set | 모델 학습용 | 약 80% |
| Validation Set | 성능 평가용 (튜닝 시 사용) | 약 20% |
| Test Set | 마지막 성능 확인용 (경쟁 제출용) | 별도 |
Train Set: 모델이 배우는 재료
Validation Set: 모델이 너무 외우고 있진 않은지 점검
Test Set: 마지막 성적표 (※ 훈련 중엔 절대 안 봐야 공정함!)
예시
- Train: 내가 문제를 푸는 연습 시간
- Validation: 친구가 준 모의고사로 실력 점검
- Test: 실제 수능 시험
첫 번째로 데이터를 학습 데이터와 검증 데이터로 나누고 학습을 하면서
학습 데이터가 적어도 유의미하게 작아지는지를 보면 된다.
Train Loss가 유의미하게 작아지지 않는다면 모델이 충분히 표현하지 않아서(단순해서) underfitting이 발생함.
그렇다면 이 경우를 넘어서, 내가 모델을 키워서 충분히 키워서 Train Loss가 꽤 작아지는 지점을 찾았을 때
그때는 과적합(overfitting)이 발생했는지, 안 했는지를 판단해야 함.
그때는 학습 데이터셋에서 발생하는 loss랑 검증 데이터셋에서 발생하는 loss의 차이가 크지 않는가?
내가 학습 데이터셋에 너무 over해서 fit 하지 않았는가를 이러한 Train Loss랑 Validation Loss를 가지고 판단하면 된다.
이런 것드을 Generalization(일반화) 능력이라고 부름.
실제로 우리가 학습 손실을 최소화하는 형태로 학습하지만 실제로 우리가 바라는 것은 실제 현장에서 이 모델이 잘 작동하는 것이 목표임.
일반적으로 사용하는 방식은 학습 데이터를 80% 정도, 검증 데이터를 20% 정도 사용해서 확인
테스트 데이터는 결국 내가 만든 모델의 성능을 발표할 때 사용한 테스트 데이터는
역시 검증 데이터가 아닌, 따로 저장되어 있는 다른 데이터를 사용해야한다.
실제로는 학습 셋과 검증 셋을 이용해서 오버피팅을 넘어서지 않으면서도 언더피팅은 넘어서는 것을 찾아낸 다음,
최종적으로 경기에 나가서 마지막 테스트 셋으로 실험하는 머릿속에 염두해두기
그럼 애매한 부분이 있을 수도 있을 것 같다
이차식이 맞나, 삼차식이 맞나? 사차식은 확실히 오버피팅이고 일차식은 확실히 언더피팅 이라면 이차식과 삼차식 중에 뭘 고를까? 이런 경우가 발생할수도 있음

이차식과 삼차식이 둘 다 유의미하다고 한다면 가급적 더 단순하면서도 간단한 모델을 사용하는 것이 여러모로 안전하다.
학습 오차와 검증 오차가 비슷해지는 형태의 모델을 찾으면 됨
학습 오차는 굉장히 작은데 검증 오차가 되게 크다면 아마도 오버피팅에 갇힌 걸거다

오버피팅이라면 첫 번째로 모델의 복합도를 낮추는 것을 할 수 있음.
7차식 -> 6차식으로 낮추던가, 데이터를 더 얻는 방법도 있는데 그건 비싸고 시간이 걸리는 일임
혹은 최근에는 생성형 샘플들을 사용하는 테크닉 제시되고 있는데,
이건 생성 모델의 성능에 의존할 수 있기 때문에 굉장히 조심하는 것이 좋다!
앞으로 나오는 내용은 정규화(Regularization)와 증강(Augmentation) 이라고 하는 테크닉인데 살펴볼 것임
그전에!!
데이터가 부족한 경우 어떻게 극복할 건데?
-> Cross Validation 테크닉
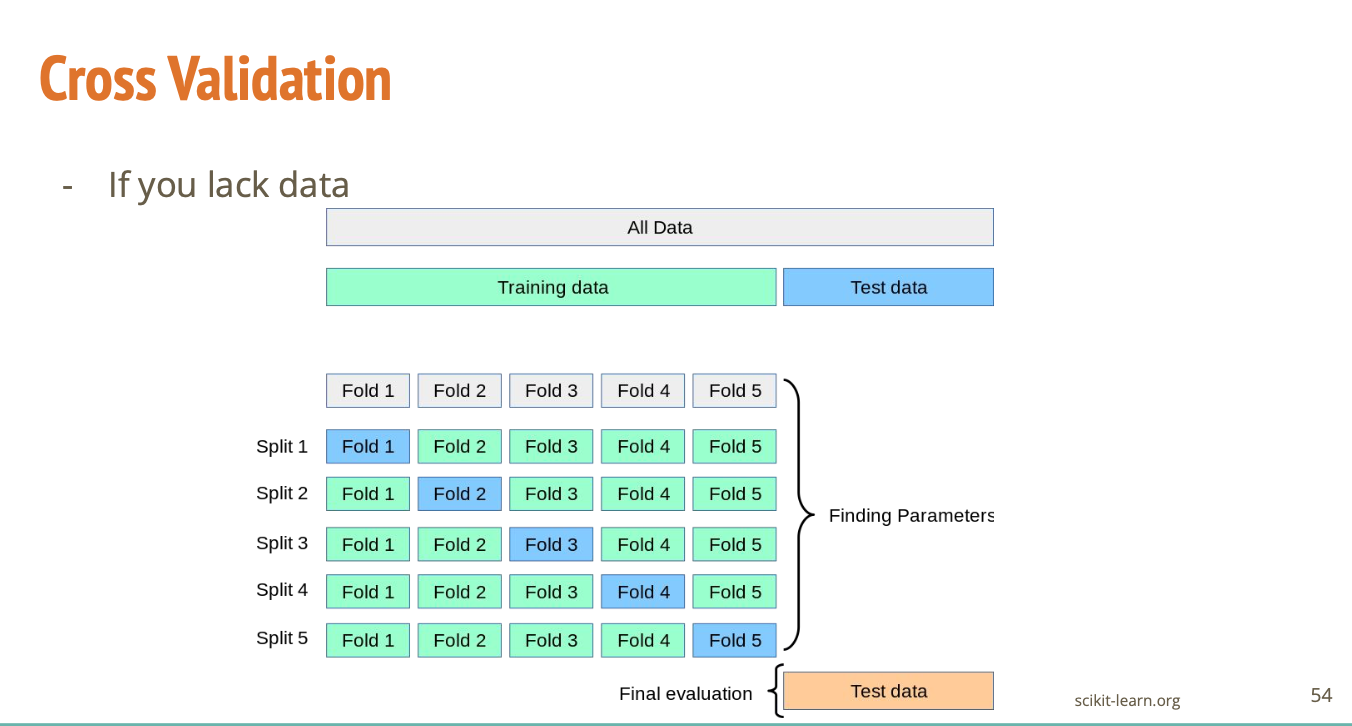
데이터가 적은 것이 고민인데 이 중에 80%만 학습에 활용하고, 20%를 검증을 위해 아껴두는 것은 아까울 수 있음.
그 경우엔 우리가 학습(Train) 데이터와 검증(Validation) 데이터 둘 다 포함한 데이터를
20%씩 다섯 개로 나누어 첫번째 학습할 땐 1번 Fold를 검증하고 나머지 네 개를 학습
두 번째 스테이지에서는 1번 Fold, 3,4,5번 Fold를 학습에 사용하고 2번 Fold로 검증
이런 식으로 총 5번 학습/검증 반복:
Split 1: Fold 1 = 검증, Fold 2~5 = 학습
Split 2: Fold 2 = 검증, Fold 1,3,4,5 = 학습
...
마지막엔 평균 성능을 평가함

우리가 훈련 손실만 너무 줄이려 하다 보면 복잡한 모델이 과적합이 되기 쉬움.
그래서 정규화는 모델이 너무 복잡해져서 훈련 데이터까지 외워버리는(overfitting) 걸 막아주는 기술
왼쪽 수식을 보면, 원래의 손실함수에다가 정규화 항을 추가한 것.
오른쪽 수식은 각 데이터에 대한 예측 오류와 모델의 가중치가 너무 크지 않도록 제약하는 것을 말함.
λ(lambda)란?
λ는 정규화의 세기를 조절하는 다이얼이에요.
- λ가 크면: 벌점이 커져서 가중치를 줄이려고 함 → 덜 외우게 함
- λ가 작으면: 벌점이 약해서 거의 영향 없음 → 외울 수도 있음

학습할 데이터가 적거나, 다양성이 부족하면 → 가짜로 데이터를 만들어서 더 많이 학습시키는 방법
강아지가 오른쪽으로 살짝 움직였다고 다른 동물인가? 아님
→ 이런 걸 이용해서 강아지 사진을 옆으로 살짝 옮긴 사진도 학습에 쓰자는 것
데이터가 적다고 했을 때 강아지 사진을 많이 찍어오는 것이 가장 좋은 방법이지만,
우리가 기존의 데이터를 증강이라고 하는 기법을 통해서 펌핑할 수 있음
여기서 중요하게 다루는 근거가 되는 내용은 우리가 일반적으로 다루는 이미지, 혹은 데이터들이 어떤 특정한 변화에 대해 불변성을 가진다는 성질 때문.
- 뒤집기 (Flip): 좌우 반전
- 늘리기 (Enlarge): 확대
- 회전 (Rotate): 약간 돌리기
- 노이즈 추가 (Add noise): 살짝 흐릿하게 만들기
- 색상 바꾸기 (Color jitter): 밝기나 색 변화 주기
강아지 사진은 옆으로 옮겨서 봐도 강아지다. 90도 회전해도 강아지는 강아지
본질적인 특성이 변하지 않는 경우엔 이미지에 이러한 변화를 주는 형태로
더 많은 입력 이미지를 생성해서 Supervised Learning 모델에게 쥐여줄 수 있음.
그렇다고 해도 아무 생각없이 적용하면 안되는게
어떤 데이터셋은 이러한 형태의 불변성이 통용되지 않는 경우가 있을 수 있기 때문
예를 들어, 숫자를 판별하는 경우 숫자 6를 회전시키면 더이상 숫자6을 6이라고 보기 어려울 수도 있음. 숫자 2도 마찬가지.
정리하면,
선형 회귀는 벡터 미분이라고 하는 기법을 이용해서 간단하게 풀 수 있는 테크닉에 대해서 소개를 함
모델을 이차, 삼차식으로 넘어간다고 해도 선형 회귀의 카테고리로 들어간다.
그러면 얼마나 복잡한 모델을 사용해야 하는가에서 발생하는 트레이드 오프가 Overfitting과 Underfitting의 트레이드 오프가 있었고,
내가 Overfitting 제도에 들어가는지, 안 들어가는지를
학습과 검증 데이터셋을 이용해서 판단할 수 있다는 내용을 살펴봤음.
추가로 데이터를 더 얻고싶은 경우에는 증강 기법을 활용해서 데이터를 더 많이 확보해서 오버피팅을 피할 수 있는 기법에 대해서도 소개했음.
'LG Aimers > AI Essential Course' 카테고리의 다른 글
| Classification (0) | 2025.07.27 |
|---|---|
| Gradient Descent (0) | 2025.07.27 |
| Supervised Learning Overview (0) | 2025.07.25 |
| 인과추론을 위한 다양한 방법과 특징 (0) | 2025.07.25 |
| 인과추론을 위한 두가지 프레임워크 (0) | 2025.07.25 |



